题目内容
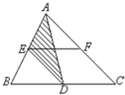已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍，那么阴影部分的面积是________平方厘米．
14
分析：①三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍，所以平行四边形DEFC的面积=56÷2=28（平方厘米）；
②△AED与平行四边形DEFC是等底等高的，根据三角形面积公式和平行四边形的面积公式可得，△AED的面积=平行四边形DEFC一半，由此即可计算得出阴影部分的面积．
解答：根据分析可得：
56÷2=28（平方厘米），
28÷2=14（平方厘米），
答：阴影部分的面积是14平方厘米．
故答案为：14．
点评：抓住图形中潜在的条件：得出等底等高的三角形与平行四边形的面积关系．
分析：①三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍，所以平行四边形DEFC的面积=56÷2=28（平方厘米）；
②△AED与平行四边形DEFC是等底等高的，根据三角形面积公式和平行四边形的面积公式可得，△AED的面积=平行四边形DEFC一半，由此即可计算得出阴影部分的面积．
解答：根据分析可得：
56÷2=28（平方厘米），
28÷2=14（平方厘米），
答：阴影部分的面积是14平方厘米．
故答案为：14．
点评：抓住图形中潜在的条件：得出等底等高的三角形与平行四边形的面积关系．
练习册系列答案
相关题目
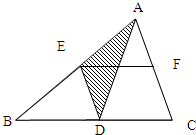如图，已知三角形ABC的面积为56平方厘米，是平行四边形DEFC面积的2倍，求阴影部分的面积．
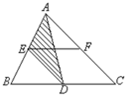已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍，那么阴影部分的面积是
如图所示，在三角形ABC中，D为BC的中点，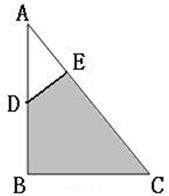
如图，已知三角形ABC的面积为15平方厘米，D为AB边中点，E为AC边三等分点，求图中阴影部分面积？