题目内容
探索规律．
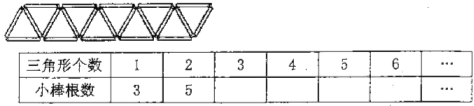
先数一数，再填一填，你能发现什么规律？
| 正方形个数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 需要小棒根数 | 4 | 7 | … |
（2）现有106根小棒，能摆多少个这样的正方形？
解：1个小正方形需要1+1×3根小棒，
2个小正方形需要1+2×3根小棒，
3个小正方形需要1+3×3根小棒…，
所以n个小正方形需要1+3n根小棒，
当n=4时，需要1+3×4=13根小棒；
当n=5时，需要1+3×5=16根小棒；
当n=6时，需要1+3×6=19根小棒；
当n=7时，需要1+3×7=22根小棒；由此即可完成上表如下：
（1）当n=16时，需要小棒1+16×3=49（根），
答：摆16个这样的正方形需要49根小棒．
（2）当1+3n=106时，
3n=105，
n=35，
答：106根小棒，能摆35个这样的正方形．
分析：观察图形可知：1个小正方形需要1+1×3根小棒，2个小正方形需要1+2×3根小棒，3个小正方形需要1+3×3根小棒…，由此找出规律解答即可．
点评：根据题干中特殊的例子，推理得出这组图形的一般规律，是解决此类问题的关键．
2个小正方形需要1+2×3根小棒，
3个小正方形需要1+3×3根小棒…，
所以n个小正方形需要1+3n根小棒，
当n=4时，需要1+3×4=13根小棒；
当n=5时，需要1+3×5=16根小棒；
当n=6时，需要1+3×6=19根小棒；
当n=7时，需要1+3×7=22根小棒；由此即可完成上表如下：
（1）当n=16时，需要小棒1+16×3=49（根），
答：摆16个这样的正方形需要49根小棒．
（2）当1+3n=106时，
3n=105，
n=35，
答：106根小棒，能摆35个这样的正方形．
分析：观察图形可知：1个小正方形需要1+1×3根小棒，2个小正方形需要1+2×3根小棒，3个小正方形需要1+3×3根小棒…，由此找出规律解答即可．
点评：根据题干中特殊的例子，推理得出这组图形的一般规律，是解决此类问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
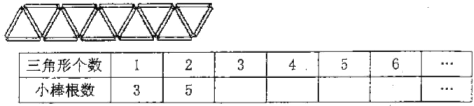
探索规律