题目内容
6.如图(1),一个长方形纸条从正方形的左边开始以每秒2厘米的速度沿水平方向向右行驶,如图(2)是运动过程中长方形纸条和正方形重叠部分的面积与运动时间的关系图.(1)运动4秒后,重叠部分的面积是多少平方厘米?
(2)正方形的边长是多少厘米?
(3)在图(2)的10,16内填入正确的时间.
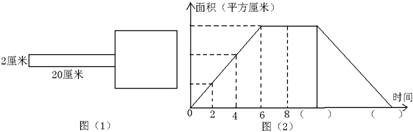
分析 (1)运行4秒后,重叠的面积是长方形,只要找出这个长方形的长和宽就能知道重叠部分的面积;
(2)从上边给出的图中,可以看出运行6秒后,重叠部分的面积不再发生变化,从而知道6秒时长方形和正方形的位置关系,6×2=12厘米,这个正方形的边长是12厘米;
(3)当长方形的前头,刚好穿过正方形时,此时长方形已经走的路程就是长方形的长20厘米;当长方形的后头刚好穿出正方形时,长方形已经走的路程就是长方形的长20厘米加上正方形的边长,然后用路程除以速度就是运行的时间.
解答 解:(1)长方形的长是:2×4=8(厘米),宽是2厘米,
重叠的面积是:8×2=16(平方厘米);
答:运行4秒后,重叠面积是16平方厘米.
(2)正方形的边长是运行6秒后的长度:6×2=12(厘米);
答:正方形的边长是12厘米.
(3)当长方形的前头,刚好穿过正方形时,
20÷2=10(秒);
长方形离开正方形时,
(20+12)÷2
=32÷2
=16(秒);
答:长方形的前头,刚好穿过正方形时,用了10秒;当长方形离开正方形时,用了18秒.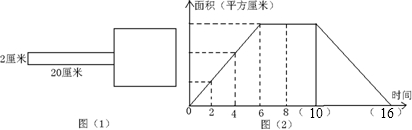
故答案为:10,16.
点评 此题综合性较强,综合考查了匀速运动这一知识,以及分析折线统计图的能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
16.下面几句话,正确的是( )
| A. | 把一个圆平均分成3份,表示其中的2份,写作$\frac{2}{3}$ | |
| B. | 把一个圆平均分成2份,表示其中的3份,写作$\frac{2}{3}$ | |
| C. | 把一个圆分成3份,每份是$\frac{1}{3}$,这样的两份,写作$\frac{2}{3}$ | |
| D. | 把一个圆分成4,每份是$\frac{1}{3}$,这样的两份,写作$\frac{4}{3}$ |
1.下面的方框架中,( )具有不易变形的特性.
| A. |  | B. |  | C. |  | D. |  |
15.右面各算式中计算结果最小的是( )
| A. | $\frac{9}{10}$÷11 | B. | 11×$\frac{9}{10}$ | C. | 11÷$\frac{9}{10}$ |
 如图是六(1)班同学英语考试成绩统计图.成绩达到或超过80分为优秀,请计算这次六(1)班英语考试的优秀率.
如图是六(1)班同学英语考试成绩统计图.成绩达到或超过80分为优秀,请计算这次六(1)班英语考试的优秀率.