题目内容
(2010?江苏模拟)一个直角三角形的三条边的长度分别为3厘米,4厘米和5厘米,以其中的某一条边为轴,将三角形旋转一周,得到的立体图形的体积最大是
50.24
50.24
立方厘米.分析:分别以直角三角形的三条边为轴,将三角形旋转一周,分别求出3个立体图形的体积,进行比较,就可以得出那个最大了.
解答:解:①、以3厘米的边为轴旋转一周如图所示,可以得到一个圆锥,
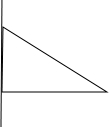
体积为:
×π×42×3=16π(平方厘米);
②、以4厘米的边为轴旋转一周如图所示,可以得到一个圆锥,
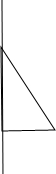
体积为:
×π×32×4=12π(平方厘米);
③、以5厘米的边为轴旋转一周如图所示,可以得到两个圆锥,
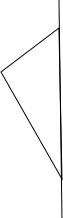
设斜边上的高为h,根据三角形的面积相等,得:3×4=5×h,
h=
(厘米),
体积为:
×π×(
)2×5=9.6π(平方厘米);
所以最大的是16π=16×3.14=50.24(立方厘米);
故答案为:50.24.

体积为:
| 1 |
| 3 |
②、以4厘米的边为轴旋转一周如图所示,可以得到一个圆锥,

体积为:
| 1 |
| 3 |
③、以5厘米的边为轴旋转一周如图所示,可以得到两个圆锥,

设斜边上的高为h,根据三角形的面积相等,得:3×4=5×h,
h=
| 12 |
| 5 |
体积为:
| 1 |
| 3 |
| 12 |
| 5 |
所以最大的是16π=16×3.14=50.24(立方厘米);
故答案为:50.24.
点评:此题考查了以三角形的三边分别旋转分别得到三个不同的圆锥,分别按圆锥体积公式计算找出最大的.

练习册系列答案
相关题目