题目内容
如果圆、正方形和长方形的周长相等,那么面积最大的是
- A.圆
- B.正方形
- C.长方形
A
分析:本题可举列解决:设圆、正方形和长方形的周长均为1,根据它们的周长及面积公式可知,(1)正方形的面积为(1÷4)×(1÷4)= ;(2)长方形的(长+宽)=1÷2=
;(2)长方形的(长+宽)=1÷2= ,如果长为
,如果长为 ,则宽为
,则宽为
 =
= ,其面积为
,其面积为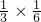 =
= ;(3)圆的周长为1,其半径为(1÷3.14÷2),面积为(1÷3.14÷2)×(1÷3.14÷2)×3.14=
;(3)圆的周长为1,其半径为(1÷3.14÷2),面积为(1÷3.14÷2)×(1÷3.14÷2)×3.14= ;因为
;因为 >
>
 ,所以,圆的面积最大.
,所以,圆的面积最大.
解答:设圆、正方形和长方形的周长均为1,根据它们的周长及面积公式可知:
(1)正方形的面积为(1÷4)×(1÷4)= ;
;
(2)长方形的(长+宽)=1÷2= ,如果长为
,如果长为 ,则宽为
,则宽为
 =
= ,其面积为
,其面积为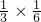 =
= ;
;
(3)圆的面积为(1÷3.14÷2)×(1÷3.14÷2)×3.14= ;
;
因为 >
>
 ,所以,圆的面积最大.
,所以,圆的面积最大.
故选:A.
点评:完成本题依据它们的周长及面积公式进行分析解决.
分析:本题可举列解决:设圆、正方形和长方形的周长均为1,根据它们的周长及面积公式可知,(1)正方形的面积为(1÷4)×(1÷4)=
 ;(2)长方形的(长+宽)=1÷2=
;(2)长方形的(长+宽)=1÷2= ,如果长为
,如果长为 ,则宽为
,则宽为
 =
= ,其面积为
,其面积为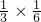 =
= ;(3)圆的周长为1,其半径为(1÷3.14÷2),面积为(1÷3.14÷2)×(1÷3.14÷2)×3.14=
;(3)圆的周长为1,其半径为(1÷3.14÷2),面积为(1÷3.14÷2)×(1÷3.14÷2)×3.14= ;因为
;因为 >
>
 ,所以,圆的面积最大.
,所以,圆的面积最大.解答:设圆、正方形和长方形的周长均为1,根据它们的周长及面积公式可知:
(1)正方形的面积为(1÷4)×(1÷4)=
 ;
;(2)长方形的(长+宽)=1÷2=
 ,如果长为
,如果长为 ,则宽为
,则宽为
 =
= ,其面积为
,其面积为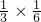 =
= ;
;(3)圆的面积为(1÷3.14÷2)×(1÷3.14÷2)×3.14=
 ;
;因为
 >
>
 ,所以,圆的面积最大.
,所以,圆的面积最大.故选:A.
点评:完成本题依据它们的周长及面积公式进行分析解决.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目