题目内容
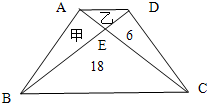 两条对角线把梯形分割成四个三角形,已知两个三角形的面积如图,求甲、乙两个三角形面积各是多少?(单位:平方厘米)
两条对角线把梯形分割成四个三角形,已知两个三角形的面积如图,求甲、乙两个三角形面积各是多少?(单位:平方厘米)分析:因为在三角形ABD与三角形DAC中,底都是AD,高都是AD与BC平行线段的距离,所以两个三角形的面积相等;进而得出甲的面积与三角形DEC的面积相等,即甲的面积是6平方厘米;再根据三角形的面积与底的关系得出BE:ED=18:6=3:1,由此即可求出乙的面积.
解答:解:因为,在三角形ABD与三角形DAC中,底都是AD,高都是AD与BC平行线段的距离,
所以,三角形ABD与三角形DAC的面积相等,
所以,甲的面积与三角形DEC的面积相等,
甲的面积是6平方厘米,
而,BE:ED=18:6=3:1,
甲的面积:乙的面积=3:1,
乙的面积是:6÷3=2(平方厘米),
答:甲的面积是6平方厘米;乙的面积是2平方厘米.
所以,三角形ABD与三角形DAC的面积相等,
所以,甲的面积与三角形DEC的面积相等,
甲的面积是6平方厘米,
而,BE:ED=18:6=3:1,
甲的面积:乙的面积=3:1,
乙的面积是:6÷3=2(平方厘米),
答:甲的面积是6平方厘米;乙的面积是2平方厘米.
点评:解答此题的关键是,利用同底等高的性质与三角形的面积与底的关系,得出面积与面积的关系,及边长与面积的关系,从而得出答案.

练习册系列答案
相关题目