题目内容
设a,b,c,d是自然数,对每两个数组(a,b),(c,d),我们定义运算※如下:(a,b)※(c,d)=(a+c,b+d);又定义运算△如下:(a,b)△(c,d)=(ac+bd,ad+bc).试计算((1,2)※(3,6))△((5,4)※(1,3)).
分析:先看第一种新的运算即※的运算意义是什么;再看第二种新的运算即△的运算意义是什么,根据此两个符号的运算意义,运用到所求的式子,即可得到答案.
解答:解:因为,(1,2)※(3,6)=(1+3,2+6)=(4,8),
(5,4)※(1,3)=(5+1,4+3)=(6,7).
所以((1,2)※(3,6))△((5,4)※(1,3)),
=(4,8)△(6,7),
=(4×6+8×7,4×7+8×6),
=(80,76).
故答案为:(80,76).
(5,4)※(1,3)=(5+1,4+3)=(6,7).
所以((1,2)※(3,6))△((5,4)※(1,3)),
=(4,8)△(6,7),
=(4×6+8×7,4×7+8×6),
=(80,76).
故答案为:(80,76).
点评:解答此题最重要的是,要彻底弄清楚新运算符号的意义,然后再利用新运算方法,来计算要求的题目.

练习册系列答案
相关题目
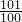 ,b=
,b=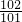 ,c=
,c=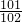 ,d=
,d=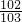 ,则a,b,c,d这四个数中,最大的是________,最小的是________.
,则a,b,c,d这四个数中,最大的是________,最小的是________.