题目内容
【题目】一个直角三角形的两条直角边分别是3cm和4cm，斜边是5cm，分别以三条边所在的直线为轴把三角形旋转一周，得到一个立体图形，比较这3个立体图形 的体积，（ ）的体积最大。
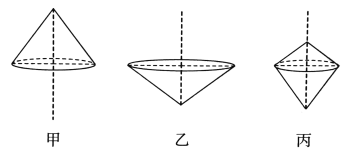
A.甲B.乙C.丙D.无法判断
【答案】B
【解析】
将直角三角形以4cm为轴旋转，得到立体图形甲，高为4cm，底面半径为3cm，再利用圆锥的体积公式代入数据解答；以3cm为轴旋转，得到立体图形乙，高为3cm，底面半径为4cm，再利用圆锥的体积公式代入数据解答；以5cm为轴旋转，得到立体图形丙，底面半径可以借助三角形的面积4×3÷2＝5×r÷2求出，进而求出底面积，进而求出两个圆锥的体积即可。分别算出体积后，进行比较即可得解。
甲的体积：
×3.14×3
×4
＝×3.14×9×4
＝37.68（立方厘米）
乙的体积：×3.14×4×3
＝×3.14×16×3
＝50.24（立方厘米）
丙的体积：
r＝3×4÷5＝2.4（厘米）
h
＋h
＝5（厘米）
×3.14×2.4×h＋×3.14×2.4×h
＝×3.14×2.4×（h＋h）
＝×3.14×2.4×5
＝30.144（立方厘米）
50.24＞37.68＞30.144，即乙的体积＞甲的体积＞丙的体积，所以乙的体积最大。
故答案为：B。
练习册系列答案
相关题目
【题目】在方框里填数，使每行里的数均相等。
用复名数表示 | 用小数表示 | 用分数表示 |
1升3毫升 | （________） | （________） |
（________） | 2.05千克 | （________） |
（________） | （________） | 3 |
4立方分米70立方厘米 | （________） | （________） |
