Question

综合与实践．
（一）　
（1）画一个边长4厘米的正方形．
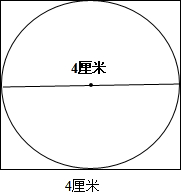
（2）在正方形中画一个最大的圆．
（3）如果在正方形中把这个圆剪掉，剩下部分的面积是多少？
（二）小刚和小强比赛跑步，他们同时从同地出发．

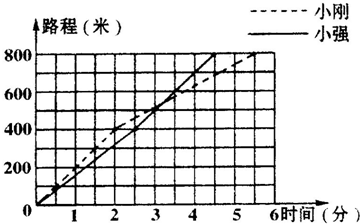
（1）________先到达终点，用了________分钟．
（2）出发________分钟后，小强追上小刚，比赛中两人相距最远约是________米．
（4）小刚的平均速度是每分________米，小强的平均速度是________米．（得数保留整数）

Answer 1

解：（一）（1）先画一条4厘米的线段，然后在线段的两端的上方，做4厘米的垂线段，最后把垂线段的上方连接即可画出4厘米的正方形；

（2）先确定圆心，即正方形对角线的交点就是圆的圆心，然后以4÷2=2厘米为半径画圆；
画图如下：

（3）4×4=16（平方厘米），
3.14×（）²=12.56（平方厘米），
16-12.56=3.44（平方厘米）；
答：剩下部分的面积是3.44平方厘米．

（二）（1）4.5＜5.5，小强先到达终点，用了4.5分钟；

（2）相距最远是出发后2分钟是，400-300=100米，
答：出发3分钟后，小强追上小刚，比赛中两人相距最远约是100米；

（3）小刚的平均速度：800÷5.5≈145（米），
小强的平均速度：800÷4.5≈178（米）；
答：小刚的平均速度是每分145米，小强的平均速度是178米．
分析：（一）（1）根据正方形的画法，画一个边长4厘米的正方形；
（2）在正方形中画一个最大的圆，就是圆的直径是正方形的边长4厘米，据此画出；
（3）如果在正方形中把这个圆剪掉，剩下部分的面积是多少，正方形的面积减去圆的面积；
（二）小刚和小强比赛跑步，他们同时从同地出发．
（1）观察统计图可知；小强跑完800米用了4.5分钟，小刚用了5.5分钟，比较两个时间哪个人哪个跑完用的时间少那个人就跑的快；
（2）小强和小刚的统计图的线相交的地方的时间，就是小强追上小刚的时间，比赛中两人相距最远就是两条折线相差最大的，求出数据即可；
（3）平均速度=路程÷时间，据此求出他们的各自平均速度．
点评：解答本题主要应用画图的方法、正方形和圆的面积公式，以及统计的知识，注意掌握正方形和圆的面积公式和平均速度的公式．