题目内容
在图中,阴影部分甲比阴影部分乙的面积少 172cm2,AB长40cm,求BC的长.(π=3.14,AB 是直径)
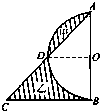

分析:由题意得:S乙=梯形面积-
圆的面积=
=
×3.14×(40÷2)2=200+10BC-314;S甲=
圆的面积-三角形面积=
×3.14×(40÷2)2-
×(40÷2)×(40÷2)=314-200=114,再根据乙的面积-甲的面积=172解答BC的长即可.
| 1 |
| 4 |
| (40÷2+BC)×(40÷2) |
| 2 |
| 90 |
| 360 |
| 1 |
| 4 |
| 90 |
| 360 |
| 1 |
| 2 |
解答:解:S乙=梯形面积-
圆的面积=
=
×3.14×(40÷2)2=200+10BC-314;
S甲=
圆的面积-三角形面积=
×3.14×(40÷2)2-
×(40÷2)×(40÷2)=314-200=114;
所以200+10BC-314-114=172,
10BC=172+314+314-200,
BC=400÷10,
BC=40.
答:BC的长是40厘米.
| 1 |
| 4 |
| (40÷2+BC)×(40÷2) |
| 2 |
| 90 |
| 360 |
S甲=
| 1 |
| 4 |
| 90 |
| 360 |
| 1 |
| 2 |
所以200+10BC-314-114=172,
10BC=172+314+314-200,
BC=400÷10,
BC=40.
答:BC的长是40厘米.
点评:解决本题的关键是利用梯形和三角形的面积关系求出BC的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012?绍兴县)在如图中,平行四边形的面积是20平方厘米,图中甲、乙、丙三个三角形的面积比是
(2012?绍兴县)在如图中,平行四边形的面积是20平方厘米,图中甲、乙、丙三个三角形的面积比是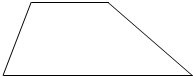 用一条线段将梯形分成甲、乙两部分,使甲、乙面积比是1:2,请在图中画出来,并将其中一部分涂上阴影.
用一条线段将梯形分成甲、乙两部分,使甲、乙面积比是1:2,请在图中画出来,并将其中一部分涂上阴影.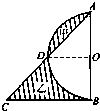
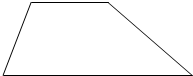 用一条线段将梯形分成甲、乙两部分,使甲、乙面积比是1:2,请在图中画出来,并将其中一部分涂上阴影.
用一条线段将梯形分成甲、乙两部分,使甲、乙面积比是1:2,请在图中画出来,并将其中一部分涂上阴影.