题目内容
 把 5个棋子放入下图中四个每条边长为“1”的小三角形内,那么一定有一个小三角形内至少有
把 5个棋子放入下图中四个每条边长为“1”的小三角形内,那么一定有一个小三角形内至少有2
2
个棋子,两棋子的距离一定小于1
1
.分析:5÷4=1…1,把 5个棋子放入下图中四个每条边长为“1”的小三角形内,每个小三角形都放上1个,余下的一个放入任何一个小三角形中,那么一定有一个小三角形内至少有 1+1=2个棋子;在同一个三角形的两棋的距离一定小于边长为“1”的小三角形的边长1.
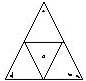

解答:解:四个每条边长为“1”的小三角形看做4个抽屉,5个棋子看做东西,5个棋子放入4个小三角形,那么一定有一个小三角形内至少有 2个棋子,两棋子的距离一定小于1.
故答案为:2,1.
故答案为:2,1.
点评:此题考查了抽屉原理,抽屉原理又称鸽巢原理,它是组合数学的一个基本原理,最先是由德国数学家狭利克雷明确地提出来的,因此,也称为狭利克雷原理.把3个苹果放进2个抽屉里,一定有一个抽屉里放了2个或2个以上的苹果.这个人所皆知的常识就是抽屉原理在日常生活中的体现.用它可以解决一些相当复杂甚至无从下手的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目