题目内容
18.如图,已知涂色部分的面积是50平方分米,求圆环的面积.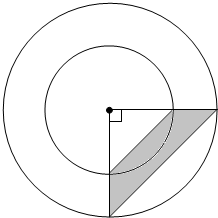
分析 根据题意,可把外圆的半径用R表示,内圆的半径用r表示,大三角形的面积为$\frac{1}{2}$R2,小三角形的面积为$\frac{1}{2}$r2,阴影面积:用大三角形的面积减去小三角形的面积,这样就能计算出(R2-r2),然后再代入圆环的面积公式S=π(R2-r2)进行计算即可得到答案.
解答 解:外圆的半径用R表示,内圆的半径用r表示,
$\frac{1}{2}$R2-$\frac{1}{2}$r2=50
$\frac{1}{2}$(R2-r2)=50
R2-r2=100
3.14×100=314(cm2);
答:圆环的面积是314平方厘米.
点评 解答此题的关键是:利用已知条件求出大小圆半径的平方之差,再据圆环面积等于大圆面积减小圆面积,即可求解.

练习册系列答案
相关题目
