题目内容
 如图,平行四边形面积为24平方厘米,则阴影部分的面积是( )平方厘米.
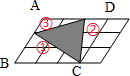
如图,平行四边形面积为24平方厘米,则阴影部分的面积是( )平方厘米.分析:由题意可知:平行四边形又被均分成了12个小平行四边形,则每个小平行四边形的面积为(24÷12)平方厘米,又因阴影部分的面积=大平行四边形的面积-空白部分的面积,于是问题得解.
解答:解:如图所示,每个小平行四边形的面积为24÷12=2(平方厘米),
则平行四边形ABCD的面积为:2×9=18(平方厘米),
空白三角形①的面积为:2×6÷2=6(平方厘米),
空白三角形②的面积为:2×3÷2=3(平方厘米),
空白三角形③的面积为:2×2÷2=2(平方厘米),
所以阴影部分的面积为:
18-(6+3+2),
=18-11,
=7(平方厘米);
答:阴影部分的面积是7平方厘米.
故选:D.
则平行四边形ABCD的面积为:2×9=18(平方厘米),
空白三角形①的面积为:2×6÷2=6(平方厘米),
空白三角形②的面积为:2×3÷2=3(平方厘米),
空白三角形③的面积为:2×2÷2=2(平方厘米),
所以阴影部分的面积为:
18-(6+3+2),
=18-11,
=7(平方厘米);
答:阴影部分的面积是7平方厘米.
故选:D.

点评:解答此题的关键是:求出每个小平行四边形的面积,进而利用S平行四边形ABCD-(S△①+S△②+S△③)即可求解.

练习册系列答案
相关题目
 (2007?抚州)如图,平行四边形面积是28平方米,求阴影部分面积.
(2007?抚州)如图,平行四边形面积是28平方米,求阴影部分面积.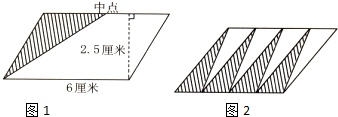
 如图,平行四边形面积是54cm2,则阴影部分面积是
如图,平行四边形面积是54cm2,则阴影部分面积是 如图,平行四边形面积是50平方厘米,底是10厘米,求阴影部分面积.
如图,平行四边形面积是50平方厘米,底是10厘米,求阴影部分面积.