题目内容
 在水渠旁用篱笆围成一块直角梯形菜地(如图),已知三面篱笆总长28米.
在水渠旁用篱笆围成一块直角梯形菜地(如图),已知三面篱笆总长28米.
(1)请试着设计几种围篱笆的方案,并分别求出这块菜地的面积.(至少写出两种方案,只要列出算式即可)
(2)篱笆怎样围时这块菜地的面积最大,最大的面积是多少平方米?
解:(1)设高为x米,则上底+下底=28-x(米),梯形面积S=(上底+下底)×高÷2=(28-x)x÷2,
方案(1)x=1米,上底+下底=28-x=28-1=27,上底取5米,则下底27-5=22米;S=27×1÷2=13.5平方米;
方案(2)x=2米,上底+下底=28-x=28-2=26,上底10米,下底26-10=16米;S=26×2÷2=26平方米;
(2)要使围成菜地的面积最大,即上底+下底=高,此时围成的面积最大,
即上底+下底=高=28÷2=14米,注意最后取数时上底+下底=14米,并且上底<下底即可;
14×14÷98(平方米),
答:最大的面积是98平方米.
分析:(1)设高为x米,则上底+下底=28-x(米),梯形面积S=(上底+下底)×高÷2=(28-x)x÷2,方案(1)x=1米,上底+下底=28-x=28-1=27,上底取5米,则下底27-5=22米;S=27×1÷2=13.5平方米;方案(2)x=2米,上底+下底=28-x=28-2=26,上底10米,下底26-10=16米;S=26×2÷2=26平方米;
(2)要使围成菜地的面积最大,即上底+下底=高,此时围成的面积最大,即上底+下底=高=28÷2=14米,注意最后取数时上底+下底=24米,并且上底<下底即可.
点评:关键是利用梯形面积S=(上底+下底)×高÷2结合本题的条件及两个数最接近时乘积最大解决问题.
方案(1)x=1米,上底+下底=28-x=28-1=27,上底取5米,则下底27-5=22米;S=27×1÷2=13.5平方米;
方案(2)x=2米,上底+下底=28-x=28-2=26,上底10米,下底26-10=16米;S=26×2÷2=26平方米;
(2)要使围成菜地的面积最大,即上底+下底=高,此时围成的面积最大,
即上底+下底=高=28÷2=14米,注意最后取数时上底+下底=14米,并且上底<下底即可;
14×14÷98(平方米),
答:最大的面积是98平方米.
分析:(1)设高为x米,则上底+下底=28-x(米),梯形面积S=(上底+下底)×高÷2=(28-x)x÷2,方案(1)x=1米,上底+下底=28-x=28-1=27,上底取5米,则下底27-5=22米;S=27×1÷2=13.5平方米;方案(2)x=2米,上底+下底=28-x=28-2=26,上底10米,下底26-10=16米;S=26×2÷2=26平方米;
(2)要使围成菜地的面积最大,即上底+下底=高,此时围成的面积最大,即上底+下底=高=28÷2=14米,注意最后取数时上底+下底=24米,并且上底<下底即可.
点评:关键是利用梯形面积S=(上底+下底)×高÷2结合本题的条件及两个数最接近时乘积最大解决问题.

练习册系列答案
相关题目
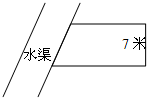 (2012?中山模拟)在一边靠水渠处,用篱笆围成一块直角梯形菜地(如图),已知三面篱笆总长27米,梯形的高为7米,则此菜地的面积是
(2012?中山模拟)在一边靠水渠处,用篱笆围成一块直角梯形菜地(如图),已知三面篱笆总长27米,梯形的高为7米,则此菜地的面积是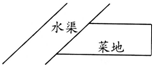 在水渠旁用篱笆围成一块直角梯形菜地(如图),已知三面篱笆总长28米.
在水渠旁用篱笆围成一块直角梯形菜地(如图),已知三面篱笆总长28米.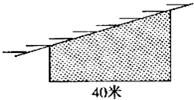 林伯伯在墙边用篱笆围成一个菜园(如图所示),围菜园的篱笆总长92米,求这个菜园的面积.
林伯伯在墙边用篱笆围成一个菜园(如图所示),围菜园的篱笆总长92米,求这个菜园的面积. 在一边靠水渠处,用篱笆围成一块直角梯形菜地(如图),已知三面篱笆总长27米,梯形的高为7米,则此菜地的面积是________平方米.
在一边靠水渠处,用篱笆围成一块直角梯形菜地(如图),已知三面篱笆总长27米,梯形的高为7米,则此菜地的面积是________平方米.