Question

一块宽是16厘米的长方形铁皮，在它的四个角分别剪去边长是4厘米的正方形，然后把它焊接成一个无盖的长方体盒子，如果这个盒子的容积是768立方厘米，那么这块铁皮原来的面积是多少平方厘米？

Answer 1

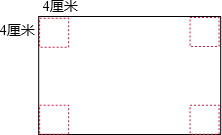
分析：如图所示，长方体盒子的体积是768立方厘米，高是4厘米，宽是（16-4×2）厘米，从而利用长方体的体积公式可以求出盒子的长，进而可以求得原铁皮的长，也就能求出这块铁皮原来的面积．

解答：解：盒子的长：
768÷[4×（16-4×2）]，
=768÷（4×8），
=768÷32，
=24（厘米），
原铁皮的长：
24+4×2，
=24+8，
=32（厘米）；
铁皮原来的面积：32×16=512（平方厘米）；
答：这块铁皮原来的面积是512平方厘米．

点评：解答此题的关键是：依据盒子的体积已知，求出盒子的长，进而求得铁皮的长，从而问题得解．