Question

15．已知S_△ABC=12，求阴影部分的面积（单位：cm）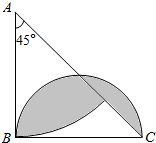

Answer 1

分析 由题意可知：阴影部分的面积=半圆的面积-半圆中空白部分的面积，而半圆中空白部分的面积等于三角形ABC的面积减去圆心角为45°，半径为三角形ABC的直角边的扇形的面积，据此利用三角形、扇形和圆的面积公式即可求解．

解答 解：设三角形ABC的直角边的长度为a，
则a×a÷2=12，
所以a²=24，
3.14×（a÷2）²÷2-（12-$\frac{45°×3.14×24}{360°}$）
=3.14×6÷2-（12-9.42）
=9.42-2.58
=6.84（平方厘米）
答：阴影部分的面积是6.84平方厘米．

点评 此题考查组合图形的面积的计算方法，一般都是转化到规则图形中，利用面积公式计算解答．