题目内容
【题目】（5分）正方形ABCD边长8厘米，等腰直角三角形EFG的斜边GF长26厘米．正方形和三角形放在同一直线上如图，CF=10厘米．正方形以每秒2厘米的速度向右沿直线运动．
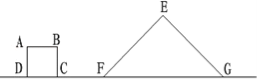
（1）第6秒时，三角形和正方形重叠的面积是多少平方厘米？
（2）第几秒时，三角形和正方形重叠的面积是62平方厘米？
【答案】（1）答：第6秒时，三角形与正方形的重叠部分面积是2平方厘米
（2）答：第12秒和15秒时，三角形和正方形重叠的面积是62平方厘米
【解析】
试题分析：（1）根据题意画图如下，正方形6秒钟移动的距离2×6=12（ 厘米），正方形与三角形EFG重叠的一条边长12﹣10=2 （厘米），进而根据三角形的面积解答；
（2）正方形的面积是8×8=64平方厘米，要使三角形和正方形重叠的面积是62平方厘米，那么有两种情况，第一种两个图形重叠后正方形的左上角还漏在外面，漏出的部分是一个面积是2平方厘米的小直角三角形；第二种情况是正方形开始离开三角形，已经漏出了正方形的右上角，漏出部分是一个面积是2平方厘米的直角三角形；
求出这两种情况三角形的直角边的长度，进而求出正方形移动的距离，再根据时间=路程÷速度求解．
解：（1）
如上图：正方形6秒钟移动的距离2×6=12（ 厘米），正方形与三角形EFG重叠的一条边长12﹣10=2 （厘米），
由于三角形FEG是等腰直角三角形，所以角EFG是45度角，
所以，重叠的小三角形也是一个等腰的直角三角形，即它的高也是2厘米（如图）
所以重叠部份的面积：2×2÷2=2 （平方厘米）；
答：第6秒时，三角形与正方形的重叠部分面积是2平方厘米．
（2）8×8=64（平方厘米）
64﹣2=2（平方厘米）
存在如下两种情况，
正方形漏出部分的面积都是2平方厘米；
因为2×2÷2=2，
所以漏出部分三角形的边长是2厘米；
第一种情况：
8﹣2=6（厘米）
正方形一共走了：10+6+8=24（厘米）
24÷2=12（秒）；
第二种情况：
正方形一共走了：10+（26﹣6）=30（厘米）
30÷2=15（秒）
答：第12秒和15秒时，三角形和正方形重叠的面积是62平方厘米．
