Question

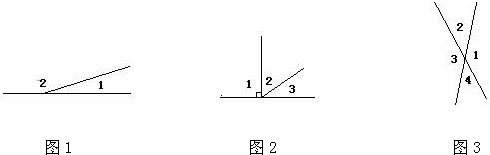
分别算出下面各图中的∠1、∠2、∠3的度数．　
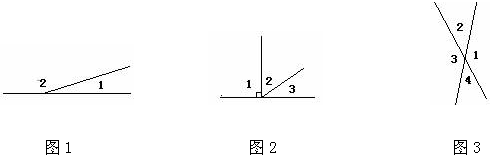
图1中，∠2=160°，∠1

20°

；
图2中，∠3=35°，∠2=

55°

；
图3中，∠1=135°，∠3=

135°

．

Answer 1

分析：（1）图形1中，∠1与∠2正好组成一个平角，所以∠1=180°-∠2；
（2）图形2中，∠2与∠3组成一个直角，所以∠2=90°-∠3；
（3）图形3中，∠1与∠3是一对对顶角，根据对顶角相等的性质即可解答．

解答：解：（1）∠1=180°-∠2=180°-160°=20°；
（2）∠2=90°-∠3=90°-35°=55°；
（3）∠1与∠3是一对对顶角，所以∠3=135°；
答：∠1=20°、∠2=55°、∠3=135°．
故答案为：20°；55°；135°．

点评：解答此类问题的关键是利用图形中已知的特殊角：平角与直角的度数进行计算解答．