Question

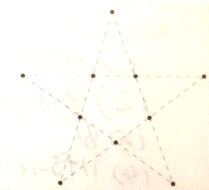一个标准的五角星（如图）由10个点连接而成，从这10个点随机选取3个点，则这三个点在同一条直线上的概率为多少，这三个点能构成三角形的概率为多少？如果选取4个点，则这四个点恰好构成平行四边形的概率为多少？

Answer 1

考点：概率的认识

专题：可能性

分析：（1）首先求出从这10个点随机选取3个点一共有多少种情况，然后判断出五条边上各有4个点，其中的任意3点都在同一条直线上，求出一共有多少种情况，再除以从这10个点随机选取3个点一共有的情况的数量，求出这三个点在同一条直线上的概率为多少；
（2）根据题意，用1减去三个点在同一条直线上的概率，求出这三个点能构成三角形的概率为多少即可；
（3）首先求出从这10个点随机选取3个点一共有多少种情况，然后判断出构成的平行四边形的个数，再除以从这10个点随机选取3个点一共有的情况的总量，求出这四个点恰好构成平行四边形的概率为多少即可．

解答： 解：（1）这三个点在同一条直线上的概率为：
（5×

C

3 4

）÷

10×9×8

3×2×1

=20÷120
=

1

6

（2）这三个点能构成三角形的概率为：
1-

1

6

=

5

6

（3）如果选取4个点，则这四个点恰好构成平行四边形的概率为：
10÷

10×9×8×7

4××2×1

=10÷210
=

1

21

答：这三个点在同一条直线上的概率为

1

6

，这三个点能构成三角形的概率为

5

6

，如果选取4个点，则这四个点恰好构成平行四边形的概率为

1

21

．

点评：此题主要考查了概率的认识，要熟练掌握事件发生的概率的求法．