题目内容
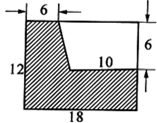
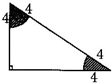
求下面组合图形中阴影部分的面积.(单位:cm)
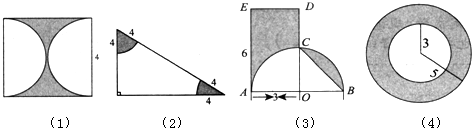
解:(1)4×4-3.14×(4÷2)2,
=16-12.56,
=3.44(平方厘米);
答:阴影部分的面积是3.44平方厘米.
(2) ×3.14×42,
×3.14×42,
= ×3.14×16,
×3.14×16,
=3.14×4,
=12.56(平方厘米);
答:阴影部分的面积是12.56平方厘米.
(3)(6-3+6)×3÷2,
=9×3÷2,
=13.5(平方厘米);
答:阴影部分的面积是13.5平方厘米.
(4)3.14×(52-32),
=3.14×(25-9),
=3.14×16,
=50.24(平方厘米);
答:阴影部分的面积是50.24平方厘米.
分析:(1)阴影部分的面积=正方形的面积-圆的面积,利用正方形和圆的面积公式即可求解;
(2)阴影部分的面积就等于圆心角为90度,半径为4厘米的扇形的面积,利用扇形面积公式即可得解;
(3)如图所示,连接AC,则空白①和阴影②的面积相等,于是阴影部分的面积就等于梯形ACDE的面积,利用梯形的面积公式即可求解;
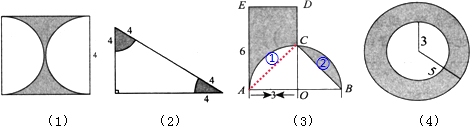
(4)阴影部分是一个圆环,大圆的面积减小圆的面积就是圆环的面积,据此即可得解.
点评:解答此题的关键是弄清楚:阴影部分的面积可以由哪些图形的面积和或差求解.
=16-12.56,
=3.44(平方厘米);
答:阴影部分的面积是3.44平方厘米.
(2)
 ×3.14×42,
×3.14×42,=
 ×3.14×16,
×3.14×16,=3.14×4,
=12.56(平方厘米);
答:阴影部分的面积是12.56平方厘米.
(3)(6-3+6)×3÷2,
=9×3÷2,
=13.5(平方厘米);
答:阴影部分的面积是13.5平方厘米.
(4)3.14×(52-32),
=3.14×(25-9),
=3.14×16,
=50.24(平方厘米);
答:阴影部分的面积是50.24平方厘米.
分析:(1)阴影部分的面积=正方形的面积-圆的面积,利用正方形和圆的面积公式即可求解;
(2)阴影部分的面积就等于圆心角为90度,半径为4厘米的扇形的面积,利用扇形面积公式即可得解;
(3)如图所示,连接AC,则空白①和阴影②的面积相等,于是阴影部分的面积就等于梯形ACDE的面积,利用梯形的面积公式即可求解;

(4)阴影部分是一个圆环,大圆的面积减小圆的面积就是圆环的面积,据此即可得解.
点评:解答此题的关键是弄清楚:阴影部分的面积可以由哪些图形的面积和或差求解.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目