题目内容
18.一个水池,底部按有一个常开的排水管,上面装有若干个一样的排水管,当打开4个进水管时,需要5小时才能注满水,当打开2个进水管时,需要15小时才能注满水池,现在需要3小时内将水池注满水,只要要开几个进水管?分析 据题意可知,水管与出水管同样粗细,当打开2个进水管时,需要15小时才能注满水池,相当于一个水管在往中注水,设池的容量为1,一个注水管的注水效率为1÷15=$\frac{1}{15}$,同样出水效率也为 $\frac{1}{15}$,故只开一进水管、一排水管池中无水,要想3小时内将水池注满应多开的进水管数为:1÷( $\frac{1}{15}$×3)+1.
解答 解:据题意可知,一个注水管的注水效率为:
1÷15=$\frac{1}{15}$;
同样出水效率也为 $\frac{1}{15}$;
要想3小时内将水池注满应多开的进水管数为:
1÷( $\frac{1}{15}$×3)+1
=5+1
=6(个)
答:至少要打开6个进水管.
故答案为:6.
点评 完成本题的关健是抓住“水管与出水管同样粗细,当打开2个进水管时,需要15小时才能注满水池”这一条件求出注水与出水的效率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.一个高30厘米的圆锥容器,盛满水倒入和它等底等高的圆柱体容器内,容器口到水面距离是( )
| A. | 10厘米 | B. | 20厘米 | C. | 30厘米 | D. | 90厘米 |
3.要形象反映化肥厂2010年下半年每月的产量情况,最好选用( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 以上答案都不对 |
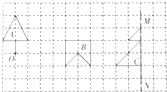 (1)画出图形A绕O点按顺时针旋转90°后得到的图形.
(1)画出图形A绕O点按顺时针旋转90°后得到的图形.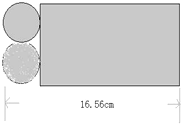 如图,一块长方形铁皮的长是16.56cm,利用图中的阴影部分刚好能做一个圆柱形油桶(接头处不计),求这个油桶的容积?
如图,一块长方形铁皮的长是16.56cm,利用图中的阴影部分刚好能做一个圆柱形油桶(接头处不计),求这个油桶的容积?