Question

12．图中D是BC的中点，E是AC的中点，三角形ABC的面积是三角形ADE面积的（　　）倍．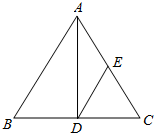

• A． 3倍
• B． 4倍
• C． 5倍
• D． 6倍

Answer 1

分析 根据D是BC的中点，E是AC的中点，可得出三角形ADC的面积等于三角形ABC面积的一半，三角形ADE的面积等于三角形ADC面积的一半，进而得解．

解答 解：因为D是BC的中点，所以S_△ADC=$\frac{1}{2}$S_△ABC，
因为E是AC的中点，所以S_△ADE=$\frac{1}{2}$S_△ADC，
所以S_△ADE=$\frac{1}{2}$S_△ADC=$\frac{1}{4}$S_△ABC，
所以三角形ABC的面积是三角形ADE面积的4倍
故选：B．

点评 此题的关键在于利用三角形面积与底的正比关系求解．