题目内容
 如图所示,∠AOB=90°,∠COB=45°,
如图所示,∠AOB=90°,∠COB=45°,(1)已知OB=20,求以OB为直径的半圆面积及扇形COB的面积;
(2)若OB的长度未知,已知阴影甲的面积为16平方厘米,能否求阴影乙的面积?若能,请直接写出结果;若不能,请说明理由.
分析:(1)我们运用圆的面积公式求出半圆的面积,用扇形的面积公式求出扇形的面积即可.
(2)我们借助第一题的解答结果,运用等量代换的方法可以求出阴影乙的面积.
(2)我们借助第一题的解答结果,运用等量代换的方法可以求出阴影乙的面积.
解答:解:(1)因为OB=20,
所以S半圆=
π×(20÷2)2,
=
π×100,
=157;
S扇形BOC=
×π×R2,
=
×π×202,
=157;
答:半圆面积是157,扇形COB的面积是157.
(2)能求阴影乙的面积:
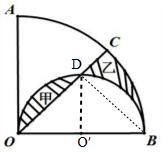
解:(1)因为,∠AOB=90°,∠COB=45°,
所以半圆的直径OB,△BOD的底是OB,
高是半圆的半径即
OB,
所以S半圆=
π×
OB×
OB,
=
πOB2;
S扇形BOC=
×π×OB2,
=
×π×OB2;
=
πOB2;
所以S半圆=S扇形BOC,
S半圆-①=S扇形-①,
所以S甲=S乙,
因为S甲=16平方厘米,
所以S乙=16平方厘米,
答:阴影乙的面积是16平方厘米.
所以S半圆=
| 1 |
| 2 |
=
| 1 |
| 2 |
=157;
S扇形BOC=
| 45 |
| 360 |
=
| 1 |
| 8 |
=157;
答:半圆面积是157,扇形COB的面积是157.
(2)能求阴影乙的面积:

解:(1)因为,∠AOB=90°,∠COB=45°,
所以半圆的直径OB,△BOD的底是OB,
高是半圆的半径即
| 1 |
| 2 |
所以S半圆=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 8 |
S扇形BOC=
| 45 |
| 360 |
=
| 1 |
| 8 |
=
| 1 |
| 8 |
所以S半圆=S扇形BOC,
S半圆-①=S扇形-①,
所以S甲=S乙,
因为S甲=16平方厘米,
所以S乙=16平方厘米,
答:阴影乙的面积是16平方厘米.
点评:本题运用圆及扇形的面积公式进行解答即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
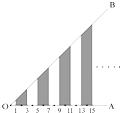 如图所示,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11,…的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,….观察图中的规律,第100个黑色梯形的面积S100=
如图所示,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11,…的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,….观察图中的规律,第100个黑色梯形的面积S100= 如图所示,∠AOB=25°,∠COD=
如图所示,∠AOB=25°,∠COD= 如图所示,∠AOB=90°,∠COB=45°,
如图所示,∠AOB=90°,∠COB=45°,