题目内容
有一个如图那样的方块网,每1个小方块里有1个人,在这些人中间,有人戴着帽子,有人没戴.每一个人都只能看见自己前方,后方和斜方的人的头,如图1所示A方块里的人能看见8个人的头,B方块里的人能看见5个人的头,C方块里的人能看见3个人的头,自己看不见自已的头.在图2的方格中,写着不同方块里的人能看见的帽子的数量,那么,请在图中找出有戴帽子的人的方块,并把它涂成黑色.
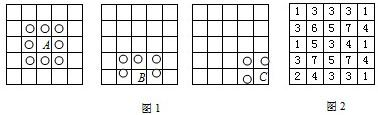

分析:此题要抓住每一个人能看到的人头的范围,并且每个人所看到的人头的情况不能相互冲突,由此逐一进行分析讨论,即可得出推理结果.
解答:解:(1)站在第一行第五列的人能看见1顶帽子,说明他周围的3人中有2人没戴帽子.
(2)站在第二行第四列的人能看见7顶帽子,说明他周围的8人中只有1人没戴帽子,综合结论可知他本人没有戴帽子.
(3)站在第二行第五列的人能看到4顶帽子,且他周围的五人中已有1人没戴帽子,说明其余4人均戴帽子,根据结论←可知他本人没戴帽子.
利用上下对称原理可以分析出:站在第四行、第五行后三列的6个人中,只有第四行第四列、第五列两人没戴帽子,其他人均戴帽子.
(4)站在第四行第二列的人能看到7顶帽子,说明他周围的8人中只有1人没戴帽子.
(5)站在第三行第1列的人能看见1顶帽子,说明他周围的5人中只有1人戴帽子.综合结论可知:这1人不可能是第二行第1、2列的人,也不可能是第四行第二列的人.所以只能是站在第三行第二列的人或第四行第1列的人.
(6)站在第五行第1列的人能看到2顶帽子,说明结论±所说戴帽子的人站在第四行第一列.
(7)站在第二行第二列的人能看到6顶帽子,说明站在第一行第1、2列的2人都戴帽子.
答:根据上述分析,可以找出有戴帽子的人的方块,并把它涂成黑色.如下图所示:

(2)站在第二行第四列的人能看见7顶帽子,说明他周围的8人中只有1人没戴帽子,综合结论可知他本人没有戴帽子.
(3)站在第二行第五列的人能看到4顶帽子,且他周围的五人中已有1人没戴帽子,说明其余4人均戴帽子,根据结论←可知他本人没戴帽子.
利用上下对称原理可以分析出:站在第四行、第五行后三列的6个人中,只有第四行第四列、第五列两人没戴帽子,其他人均戴帽子.
(4)站在第四行第二列的人能看到7顶帽子,说明他周围的8人中只有1人没戴帽子.
(5)站在第三行第1列的人能看见1顶帽子,说明他周围的5人中只有1人戴帽子.综合结论可知:这1人不可能是第二行第1、2列的人,也不可能是第四行第二列的人.所以只能是站在第三行第二列的人或第四行第1列的人.
(6)站在第五行第1列的人能看到2顶帽子,说明结论±所说戴帽子的人站在第四行第一列.
(7)站在第二行第二列的人能看到6顶帽子,说明站在第一行第1、2列的2人都戴帽子.
答:根据上述分析,可以找出有戴帽子的人的方块,并把它涂成黑色.如下图所示:

点评:此题是一个推理过程繁琐的问题,只要抓住“每一个人能看到的人头的范围,并且每个人所看到的人头的情况不能相互冲突”,即可推理得出.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目