题目内容
 在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍?
在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍?
解:[(a+ a)2-2×
a)2-2× a2]÷[
a2]÷[ a2+
a2+ -a2],
-a2],
=2(1+ )÷(1+
)÷(1+ ),
),
=2(倍),
答:正八边形的面积是阴影部分面积的2倍.
分析:如图:设正八边形ABCDEFGH的边长为a,DL的长度是 a,则正方形KLMN的面积是
a,则正方形KLMN的面积是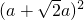 ,正八边形ABCDEFGH的面积是
,正八边形ABCDEFGH的面积是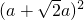 -2×
-2× a2,里面空白的小正方形的面积是a2,正方形ACEG的面积:2a2+
a2,里面空白的小正方形的面积是a2,正方形ACEG的面积:2a2+ ,所以阴影部分的面积是:
,所以阴影部分的面积是: a2+
a2+ -a2,用正八边形的面积除以阴影部分面积即可.
-a2,用正八边形的面积除以阴影部分面积即可.

点评:关键是添加辅助线,运用勾股定理求出正八边形的面积与阴影部分的面积.
 a)2-2×
a)2-2× a2]÷[
a2]÷[ a2+
a2+ -a2],
-a2],=2(1+
 )÷(1+
)÷(1+ ),
),=2(倍),
答:正八边形的面积是阴影部分面积的2倍.
分析:如图:设正八边形ABCDEFGH的边长为a,DL的长度是
 a,则正方形KLMN的面积是
a,则正方形KLMN的面积是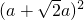 ,正八边形ABCDEFGH的面积是
,正八边形ABCDEFGH的面积是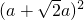 -2×
-2× a2,里面空白的小正方形的面积是a2,正方形ACEG的面积:2a2+
a2,里面空白的小正方形的面积是a2,正方形ACEG的面积:2a2+ ,所以阴影部分的面积是:
,所以阴影部分的面积是: a2+
a2+ -a2,用正八边形的面积除以阴影部分面积即可.
-a2,用正八边形的面积除以阴影部分面积即可.
点评:关键是添加辅助线,运用勾股定理求出正八边形的面积与阴影部分的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直接写数:
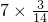 = = | 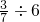 = = | 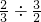 = = | 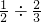 = = | 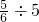 = = |
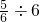 = = | 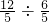 = = |  = = | 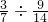 = = |  = = |
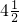 倍是1,这个数是多少?
倍是1,这个数是多少? =
= ×
× =
= =
= ÷
÷ ÷3=
÷3= =
= =
= 在一块梯形的菜园中间有一个三角形的水池,其余的地方都种菜,菜地的面积有多少平方米?
在一块梯形的菜园中间有一个三角形的水池,其余的地方都种菜,菜地的面积有多少平方米?