题目内容
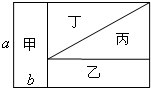 如图所示,长方形草地ABCD被分成面积相等的甲、乙、丙、丁四块,其中图形甲的长和宽的比是a:b=5:2,问图形乙的长和宽的比是多少?
如图所示,长方形草地ABCD被分成面积相等的甲、乙、丙、丁四块,其中图形甲的长和宽的比是a:b=5:2,问图形乙的长和宽的比是多少?分析:a:b=5:2,设a是5,那么b就是2;长方形乙长是c,宽是d,那么乙的面积就是c×d,直角三角形丙的面积是:
×(a-d)×c,由乙和丙的面积相等,求出d的长度;再根据甲乙的面积相等求出c,然后作比即可
| 1 |
| 2 |

解答:解:设a是5,那么b就是2;长方形乙长是c,宽是d;由乙和丙的面积相等可知:
c×d=
×(a-d)×c,
d=
(a-d),
2d=a-d,
3d=a,
a=5,所以d=
;
由甲与乙的面积相等可知:
5×2=
×c,
c=6;
所以c:d=6:
=18:5.
答:长方形乙长和宽的比是18:5.
c×d=
| 1 |
| 2 |
d=
| 1 |
| 2 |
2d=a-d,
3d=a,
a=5,所以d=
| 5 |
| 3 |
由甲与乙的面积相等可知:
5×2=
| 5 |
| 3 |
c=6;
所以c:d=6:
| 5 |
| 3 |
答:长方形乙长和宽的比是18:5.
点评:本题抓住四个图形的面积相等这一条件,进行推算出长方形乙的长和宽,即可求解.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
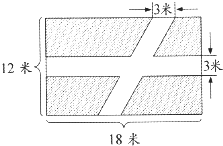 如图所示,一块长方形的草地,长18米,宽12米,中间修两条交叉的小路:一条为平行四边形,一条为长方形.求草地的实际面积.
如图所示,一块长方形的草地,长18米,宽12米,中间修两条交叉的小路:一条为平行四边形,一条为长方形.求草地的实际面积. (2008?资中县)在一长方形草地里有一条宽1米的曲折小路,如图所示,草坪的面积是
(2008?资中县)在一长方形草地里有一条宽1米的曲折小路,如图所示,草坪的面积是
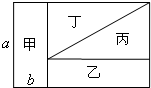 如图所示,长方形草地ABCD被分成面积相等的甲、乙、丙、丁四块,其中图形甲的长和宽的比是a:b=5:2,问图形乙的长和宽的比是多少?
如图所示,长方形草地ABCD被分成面积相等的甲、乙、丙、丁四块,其中图形甲的长和宽的比是a:b=5:2,问图形乙的长和宽的比是多少?