题目内容
将1至9这九个自然数分成两组,使其中一组各数之和是另一组各数之和的8倍,共有
3
3
种不同的分法.分析:根据题意,这两组的和就是1到9的和,再根据和倍公式求出较小一组的和,然后再进一步解答即可.
解答:解:根据题意可得:
这两组的和为:1+2+3+…+9=45;
较小一组的和为:45÷(8+1)=5;
在1至9中,和是5的有5,1+4=5,2+3=5,共有3种.
答:共有3种不同的分法.
故答案为:3.
这两组的和为:1+2+3+…+9=45;
较小一组的和为:45÷(8+1)=5;
在1至9中,和是5的有5,1+4=5,2+3=5,共有3种.
答:共有3种不同的分法.
故答案为:3.
点评:本题的关键是根据和倍公式求出较小一组的和,然后再进一步解答即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
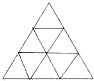 将1至9这九个自然数填人如图的九个小三角形中,使得由四个小三角形构成的三角形内的四个数之和都等于23.
将1至9这九个自然数填人如图的九个小三角形中,使得由四个小三角形构成的三角形内的四个数之和都等于23.