题目内容
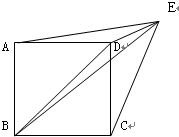 已知△ADE、△CDE和正方形ABCD面积之比是2:3:8.且△BDE的面积是4平方米,则四边形ABCD的面积是多少?
已知△ADE、△CDE和正方形ABCD面积之比是2:3:8.且△BDE的面积是4平方米,则四边形ABCD的面积是多少?
解:因为△ADE,△CDE和正方形ABCD的面积之比为2:3:8,
则设S△ADE=2x,S△CDE=3x,S△ABD=S△BCD=4x,
因为E到BC的距离=E到AD的距离+D到BC的距离,AD=BC,
所以S△EBC=S△EAD+S△DBC=2x+4x=6x,
所以S△EDB=S△EDC+S△DBC-S△EBC=3x+4x-6x=x=4(平方厘米),
所以四边形ABCE的面积是2x+3x+4x+4x=13x=13×4=52(平方厘米).
答:四边形ABCD的面积是52平方厘米.
分析:要想求出四边形ABCD的面积,就要利用题目中所给的条件,推出四边形ABCD与其它图形之间的关系.
点评:本题考查了组合图形的面积,采用设数的方法进行解答就会变得简便易行,也使我们很好理解.
则设S△ADE=2x,S△CDE=3x,S△ABD=S△BCD=4x,
因为E到BC的距离=E到AD的距离+D到BC的距离,AD=BC,
所以S△EBC=S△EAD+S△DBC=2x+4x=6x,
所以S△EDB=S△EDC+S△DBC-S△EBC=3x+4x-6x=x=4(平方厘米),
所以四边形ABCE的面积是2x+3x+4x+4x=13x=13×4=52(平方厘米).
答:四边形ABCD的面积是52平方厘米.
分析:要想求出四边形ABCD的面积,就要利用题目中所给的条件,推出四边形ABCD与其它图形之间的关系.
点评:本题考查了组合图形的面积,采用设数的方法进行解答就会变得简便易行,也使我们很好理解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
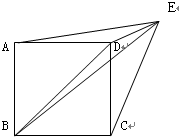 已知△ADE、△CDE和正方形ABCD面积之比是2:3:8.且△BDE的面积是4平方米,则四边形ABCD的面积是多少?
已知△ADE、△CDE和正方形ABCD面积之比是2:3:8.且△BDE的面积是4平方米,则四边形ABCD的面积是多少?