题目内容
【题目】把1到1997这1997个数,按顺时针方向依次排列在一个圆圈上(如图).从1开始按顺时针方向,保留1,擦去2;保留3,擦去4;…(每隔一个数,擦去一个数)转圈擦下去,最后剩的是哪个数?
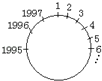
【答案】最后剩下的数应是1947
【解析】
试题分析:如果依照题意在上图中进行操作,直到剩下一个数为止,实在是很困难的.我们还应从最简单的情况入手分析,归纳出解决问题的规律,再用此规律解题.
解:如果是2个数1,2,最后剩下1;如果是3个数1,2,3,最后剩下3;如果是4个数1,2,3,4,最后剩下1;如果是5个数1,2,3,4,5,最后剩下3;如果是6个数1,2,3,4,5,6,最后剩下5;如果是1﹣7,7个数,最后剩下7;如果是1﹣8,8个数,最后剩下1.
我们发现当数的个数是2,4,8时,最后剩下的都是1.实际上,当数的个数为2n时(n≥2),当擦完一圈后还剩2n﹣1个数,把问题化成2n﹣1个数的情况.不断作下去,最后化为2个数的情况,显然最后剩下的数为1(1为起始数).
由于210=1024,211=2048,210<1997<211,1997﹣1024=973.
这就是说,要剩210个数,需要先擦去973个数.按题意,每两个数擦去一个数,当擦第973个数时,最后擦去的数是:973×2=1946.
下一个起始数是1947,所以,最后剩下的数应是1947.

【题目】按照“四舍五入”法求出商的近似值,并填入下表中.
保留一位小数 | 保留两位小数 | 保留三位小数 | |
0.68÷0.95 | _________ | _________ | _________ |
6.5÷0.27 | _________ | _________ | _________ |
589.76÷17 | _________ | _________ | _________ |