题目内容
如图所示，有一个梯形ABCD，对角线AC与BD互相垂直，AC长为16cm，BD长为12cm．这时，梯形ABCD的高AH为几厘米？
解：过点D作DE∥AC交BC的延长线于E
因为BD⊥AC，AC=16cm
所以DE⊥BD，DE=AC=16．
所以BE2=BD2+DE2=122+162=400，
所以BE=20厘米，
因为S△BDE=
AC?BD=16×12×=96（平方厘米），
所以此梯形的高是：2×96÷20=9.6（厘米），
答：梯形ABCD的高AH为9.6厘米．
分析：此题中要作辅助线：平移对角线，即过点D作DE∥AC交BC的延长线于E，则DE⊥BD，DE=AC=16厘米，由此求出BE，再根据直角三角形斜边上的高等于两条直角边的乘积÷斜边，进而求出梯形的高．
点评：本题利用了梯形、平行四边形的判定和性质、三角形的面积公式等知识．关键是作辅助线，构造平行四边形．
因为BD⊥AC，AC=16cm
所以DE⊥BD，DE=AC=16．
所以BE2=BD2+DE2=122+162=400，
所以BE=20厘米，
因为S△BDE=
AC?BD=16×12×=96（平方厘米），所以此梯形的高是：2×96÷20=9.6（厘米），
答：梯形ABCD的高AH为9.6厘米．
分析：此题中要作辅助线：平移对角线，即过点D作DE∥AC交BC的延长线于E，则DE⊥BD，DE=AC=16厘米，由此求出BE，再根据直角三角形斜边上的高等于两条直角边的乘积÷斜边，进而求出梯形的高．
点评：本题利用了梯形、平行四边形的判定和性质、三角形的面积公式等知识．关键是作辅助线，构造平行四边形．
练习册系列答案
发散思维新课堂系列答案
相关题目
有一块梯形园林地（如图所示），如果上底增加30米，下底增加25米，就构成了一个周长为360米的正方形林地，原来梯形林地的面积是多少？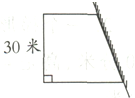
用篱笆围成一个梯形养兔场（如图所示），一边利用房屋墙壁，篱笆全长80米，养兔场面积有多大？
如图所示，有一个梯形ABCD，对角线AC与BD互相垂直，AC长为16cm，BD长为12cm．这时，梯形ABCD的高AH为几厘米？
有一块梯形园林地（如图所示），如果上底增加30米，下底增加25米，就构成了一个周长为360米的正方形林地，原来梯形林地的面积是多少？