题目内容
【题目】如图,长方体![]() 中,
中, ![]() 与底面
与底面![]() 所成的角为
所成的角为![]() .
.
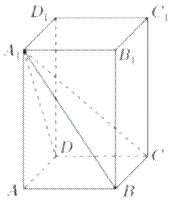
(1)求四棱锥![]() 的体积;
的体积;
(2)求异面直线![]() 与
与 ![]() 所成角的大小.
所成角的大小.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先证明![]() 是
是![]() 与底面
与底面![]() 所成的角,可得
所成的角,可得![]() ,利用棱锥的体积公式可得结果;(2)由
,利用棱锥的体积公式可得结果;(2)由![]() ,可得
,可得![]() 是异面直线
是异面直线![]() 与
与![]() 所成角(或所成角的补角),利用余弦定理可得结果.
所成角(或所成角的补角),利用余弦定理可得结果.
试题解析:(1)∵长方体ABCD﹣A1B1C1D1中,AB=BC=2,
∴AA1⊥平面ABCD,AC=![]() =2
=2![]() ,
,
∴∠A1CA是A1C与底面ABCD所成的角,
∵A1C与底面ABCD所成的角为60°,
∴∠A1CA=60°,∴AA1=ACtan60°=2![]()
![]() =2
=2![]() ,
,
∵S正方形ABCD=AB×BC=2×2=4,
∴四棱锥A1﹣ABCD的体积:
V=![]() =
=![]() =
=![]() .
.
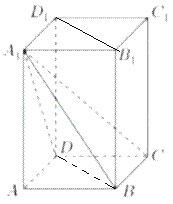
(2)∵BD∥B1D1,
∴∠A1BD是异面直线A1B与B1D1所成角(或所成角的补角).
∵BD=![]() ,A1D=A1B=
,A1D=A1B=![]() =2
=2![]() ,
,
∴cos∠A1BD=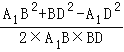 =
=![]() =
=![]() .
.
∴∠A1BD=arccos![]() .
.
∴异面直线A1B与 B1D1所成角是arccos![]() .
.
【方法点晴】本题主要考查异面直线所成的角立及棱锥的体积公式,属于中档题.求异面直线所成的角主要方法有两种:一是向量法,根据几何体的特殊性质建立空间直角坐标系后,分别求出两直线的方向向量,再利用空间向量夹角的余弦公式求解;二是传统法,利用平行四边形、三角形中位线等方法找出两直线成的角,再利用平面几何性质求解.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
【题目】光明小学一至六年级学生为“希望工程”捐款情况统计如下:
年级 | 一 | 二 | 三 | 四 | 五 | 六 |
人民币/元 | 146 | 218 | 165 | 387 | 490 | 485 |
(1)哪个年级捐款最多?哪个年级捐款最少?相差多少元?
(2)五年级比四年级多捐款多少元?
