题目内容
 如图所求,AB=24(厘米),长方形BDEF中EF=15(厘米),阴影△BCE的面积是60平方厘米,则△DCE的面积是________平方厘米.
如图所求,AB=24(厘米),长方形BDEF中EF=15(厘米),阴影△BCE的面积是60平方厘米,则△DCE的面积是________平方厘米.
30
分析:AB和EF的长度已知,于是可以求出三角形ABE的面积,又因三角形BCE的面积为60平方厘米,进而求出三角形ABC的面积,于是就能求出BC的长度,也就能求出DE的长度,进而求出三角形DCE的面积.
解答:三角形ABC的面积:24×15÷2-60,
=180-60,
=120(平方厘米);
BC的长度:120×2÷24,
=240÷24,
=10(厘米);
所以DC的长度为:15-10=5(厘米);
DE的长度:60×2÷10=12(厘米);
所以三角形DCE的面积为:5×12÷2=30(平方厘米);
答:△DCE的面积是30平方厘米.
故答案为:30.
点评:利用三角形的面积公式求得DE、DC的长度,是解答本题的关键.
分析:AB和EF的长度已知,于是可以求出三角形ABE的面积,又因三角形BCE的面积为60平方厘米,进而求出三角形ABC的面积,于是就能求出BC的长度,也就能求出DE的长度,进而求出三角形DCE的面积.
解答:三角形ABC的面积:24×15÷2-60,
=180-60,
=120(平方厘米);
BC的长度:120×2÷24,
=240÷24,
=10(厘米);
所以DC的长度为:15-10=5(厘米);
DE的长度:60×2÷10=12(厘米);
所以三角形DCE的面积为:5×12÷2=30(平方厘米);
答:△DCE的面积是30平方厘米.
故答案为:30.
点评:利用三角形的面积公式求得DE、DC的长度,是解答本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
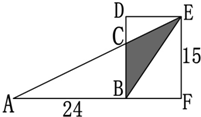 如图所求,AB=24(厘米),长方形BDEF中EF=15(厘米),阴影△BCE的面积是60平方厘米,则△DCE的面积是
如图所求,AB=24(厘米),长方形BDEF中EF=15(厘米),阴影△BCE的面积是60平方厘米,则△DCE的面积是