摘要:10.解析:-192.本题考查了简单定积分的计算以及求二项式展开式的指定项的基本方法.==2 , T= 2x
网址:http://m.1010jiajiao.com/timu_id_94844[举报]
(10分)(本题192班必做题,其他班不做)
已知二次函数f(x)=ax2+bx+c,若f(x)+f(x+1)=2x2-2x+13
(1)求函数f(x)的解析式;
(2)画该函数的图象;
(3)当x∈[t,5]时,求函数f(x)的最大值.
查看习题详情和答案>>
已知函数f(x)=
(a>0且a≠1),设函数g(x)=f(x-
)+1.
(1)求证:f(x)是奇函数;
(2)求g(x)+g(1-x)及g( 0 )+g(
)+g(
)+g(
)+g( 1 )的值;
(3)是否存在正整数a,使不等式
>n2对一切n∈N*都成立,若存在,求出正整数a的最小值;不存在,说明理由;
(4)结合本题加以推广:设F(x)是R上的奇函数,请你写出一个函数G(x)的解析式;并根据第(2)小题的结论,猜测函数G(x)满足的一般性结论.
查看习题详情和答案>>
| ax-1 |
| ax+1 |
| 1 |
| 2 |
(1)求证:f(x)是奇函数;
(2)求g(x)+g(1-x)及g( 0 )+g(
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
(3)是否存在正整数a,使不等式
| ||
| g(1-n) |
(4)结合本题加以推广:设F(x)是R上的奇函数,请你写出一个函数G(x)的解析式;并根据第(2)小题的结论,猜测函数G(x)满足的一般性结论.
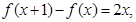 且f(0)=1.
且f(0)=1.
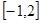 上求y= f(x)的值域。
上求y= f(x)的值域。 用一块钢锭浇铸一个厚度均匀,且全面积为2平方米的正四棱锥形有盖容器(如图),设容器的高为h米,盖子边长为a米.
用一块钢锭浇铸一个厚度均匀,且全面积为2平方米的正四棱锥形有盖容器(如图),设容器的高为h米,盖子边长为a米.