摘要:法二: .当时.且时..在为凹函数.--------------13分
网址:http://m.1010jiajiao.com/timu_id_92539[举报]
.已知定义在R上的二次函数 满足
满足 ,且
,且 的最小值
的最小值
为0,函数 ,又函数
,又函数 。
。
(I)求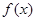 的单调区间; (II)当
的单调区间; (II)当 ≤
≤ 时,若
时,若 ,求
,求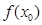 的最小值;
的最小值;
(III)若二次函数 图象过(4,2)点,对于给定的函数
图象过(4,2)点,对于给定的函数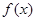 图象上的点A(
图象上的点A( ),
),
当 时,探求函数
时,探求函数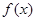 图象上是否存在点
图象上是否存在点 (
( )(
)( ),使
),使 、
、 连线平行于
连线平行于 轴,并说明理由。(参考数据:e=2.71828…)
轴,并说明理由。(参考数据:e=2.71828…)
查看习题详情和答案>>
已知定义在R上的二次函数 满足
满足 ,且
,且 的最小值为0,函数
的最小值为0,函数 ,又函数
,又函数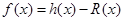 。
。
(I)求 的单调区间;
的单调区间;
(II)当 ≤
≤ 时,若
时,若 ,求
,求 的最小值;
的最小值;
(III)若二次函数 图象过(4,2)点,对于给定的函数
图象过(4,2)点,对于给定的函数 图象上的点A(
图象上的点A( ),当
),当 时,探求函数
时,探求函数 图象上是否存在点B(
图象上是否存在点B( )(
)( ),使A、B连线平行于x轴,并说明理由。
),使A、B连线平行于x轴,并说明理由。
(参考数据:e=2.71828…)
查看习题详情和答案>>












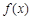 是最小正周期为
是最小正周期为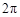 的偶函数,
的偶函数,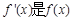 的导函数,当
的导函数,当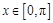 时,
时,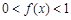 ;当
;当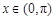 且
且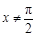 时,
时,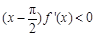 ,则方程
,则方程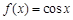 在
在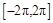 上的根的个数为( )
上的根的个数为( )