摘要:(3)假设存在.平面的法向量
网址:http://m.1010jiajiao.com/timu_id_86123[举报]
(本小题满分14分)
已知定义在 的函数
的函数 同时满足以下三条:①对任意的
同时满足以下三条:①对任意的 ,总有
,总有 ;②
;② ;③当
;③当 时,总有
时,总有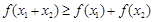 成立.
成立.
(1)函数 在区间
在区间 上是否同时适合①②③?并说明理由;
上是否同时适合①②③?并说明理由;
(2)设 ,且
,且 ,试比较
,试比较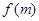 与
与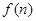 的大小;
的大小;
(3)假设存在 ,使得
,使得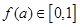 且
且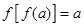 ,求证:
,求证: .
.
查看习题详情和答案>>
在平面直角坐标系xOy中,动点P到两点(-
,0),(
,0)的距离之和等于4,设点P的轨迹为曲线C,直线l过点E(-1,0)且与曲线C交于A,B两点.
(1)求曲线C的轨迹方程;
(2)若AB中点横坐标为-
,求直线AB的方程;
(3)是否存在△AOB面积的最大值,若存在,求出△AOB的面积;若不存在,说明理由.
查看习题详情和答案>>
| 3 |
| 3 |
(1)求曲线C的轨迹方程;
(2)若AB中点横坐标为-
| 1 |
| 2 |
(3)是否存在△AOB面积的最大值,若存在,求出△AOB的面积;若不存在,说明理由.
直角坐标平面中,过点A1(1,0)作函数f(x)=x2(x>0)的切线l1,其切点为B1(x1,y1);过点A2(x1,0)作函数g(x)=ex(x>0)的切线l2,其切点为B2(x2,y2);过点A3(x2,0)作函数f(x)=x2(x>0)的切线l3,其切点为B3(x3,y3);如此下去,即过点A2k-2(x2k-2,0)作函数f(x)=x2(x>0)的切线l2k-1,其切点为B2k-1(x2k-1,y2k-1);过点A2k-1(x2k-1,0)作函数g(x)=ex(x>0)的切线l2k,其切点为B2k(x2k,y2k);….
(1)求x2k-2与x2k-1及x2k-1与x2k的关系;
(2)求数列{xn}通项公式xn;
(3)是否存在实数t,使得对于任意的自然数n,不等式
+
+
+…+
+1≤t-
恒成立?若存在,求出这样的实数t的取值范围;若不存在,则说明理由.
查看习题详情和答案>>
(1)求x2k-2与x2k-1及x2k-1与x2k的关系;
(2)求数列{xn}通项公式xn;
(3)是否存在实数t,使得对于任意的自然数n,不等式
| 1 |
| x2+1 |
| 2 |
| x4+1 |
| 3 |
| x6+1 |
| n |
| x2n+1 |
| 6 |
| t |
已知向量
=(1,3),
=(m,2m-3),若对于平面内任意一向量
,都存在唯一实数对(λ,μ),使
=λ
+μ
,则实数m的取值范围是( )
| a |
| b |
| c |
| c |
| a |
| b |
| A、(-2,-3) |
| B、(-3,+∞) |
| C、(-∞,-3)∪(-3,+∞) |
| D、[-2,-3) |
 (2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.
(2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.