摘要:∴------4分
网址:http://m.1010jiajiao.com/timu_id_86115[举报]
下列有关平面向量分解定理的四个命题中,所有正确命题的序号是_______(填写命题所对应的序号即可)
(1)一个平面内有且只有一对不平行的可作为表示该平面所有的基;
(2)一个平面内有无数多对不平行可作为表示该平面内所有的基;
(3)平面的基可能互相垂直;
(4)一个平面内任一非零都可唯一地表示成该平面内三个互不平行的线性组合.
(1)一个平面内有且只有一对不平行的可作为表示该平面所有的基;
(2)一个平面内有无数多对不平行可作为表示该平面内所有的基;
(3)平面的基可能互相垂直;
(4)一个平面内任一非零都可唯一地表示成该平面内三个互不平行的线性组合.
直角坐标系下,O为坐标原点,定点E(8,0),动点M(x,y)满足
•
=x2,
(1)求动点M(x,y)的轨迹C的方程;
(2)过定点F(2,0)作互相垂直的直线l1,l2分别交轨迹C于点M,N和点R,Q,求四边形MRNQ面积的最小值;
(3)定点P(2,4),动点A,B是轨迹C上的三个点,且满足KPA•KPB=8试问AB所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由. 查看习题详情和答案>>
| MO |
| ME |
(1)求动点M(x,y)的轨迹C的方程;
(2)过定点F(2,0)作互相垂直的直线l1,l2分别交轨迹C于点M,N和点R,Q,求四边形MRNQ面积的最小值;
(3)定点P(2,4),动点A,B是轨迹C上的三个点,且满足KPA•KPB=8试问AB所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由. 查看习题详情和答案>>
直角坐标系下,O为坐标原点,定点E(8,0),动点M(x,y)满足
•
=x2,
(1)求动点M(x,y)的轨迹C的方程;
(2)过定点F(2,0)作互相垂直的直线l1,l2分别交轨迹C于点M,N和点R,Q,求四边形MRNQ面积的最小值;
(3)定点P(2,4),动点A,B是轨迹C上的三个点,且满足KPA•KPB=8试问AB所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由.
查看习题详情和答案>>
| MO |
| ME |
(1)求动点M(x,y)的轨迹C的方程;
(2)过定点F(2,0)作互相垂直的直线l1,l2分别交轨迹C于点M,N和点R,Q,求四边形MRNQ面积的最小值;
(3)定点P(2,4),动点A,B是轨迹C上的三个点,且满足KPA•KPB=8试问AB所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由.
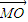 •
•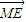 =x2,
=x2,