摘要：(Ⅱ)若.且在区间上为减函数.求实数a的取值范围,
网址：http://m.1010jiajiao.com/timu_id_85979[举报]
一、选择题： CCDBACAB
二、填空题：
9、1； 10、
；假； 11、2；
12、[0，2]；
13、
； 14、
； 15、
； 16、①、③
三、解答题：
17、解：（Ⅰ）
分
（Ⅱ）
18、解：（Ⅰ）偶函数 …………4分
（Ⅱ）（略） …………8分
（Ⅲ）① 2 …………10分
② 
…………12分
19、解：（Ⅰ）（略）用定义或导数证明 …………8分
（Ⅱ）
20、解：（Ⅰ）
21、解：（Ⅰ）在
图象上任取一点(x,y)，则(x,y)关于(0,1)的对称点为(-x,2-y)
由题意得：
（Ⅱ）
且
在
（Ⅲ）（略）………………………………14分
22、解：（Ⅰ）的不动点是-1，2 ………………3分
（Ⅱ）由
得：
， 由已知，此方程有相异二实根
（Ⅲ）设A（x1,y1）, B(x2,y2) 直线
是线段AB的垂直平分线， 
令AB的中点
，由（Ⅱ）知
（当且仅当
时，取等号） 又
函数y=f（x）在区间（0，+∞）内可导．导函数f′（x）是减函数，且f′（x）＞0，x0∈（0，+∞）．g（x）=kx+m是y=f（x）在点（x0，f（x0））处的切线方程．
（1）用x0，f（x0），f′（x0）表示m；
（2）证明：当x∈（0，+∞）时，g（x）≥f（x）；
（3）若关于x的不等式x2+1≥ax+b≥
x
在（0，+∞）上恒成立，其中a，b为实数，求b的取值范围及a，b所满足的关系．
查看习题详情和答案>>
（1）用x0，f（x0），f′（x0）表示m；
（2）证明：当x∈（0，+∞）时，g（x）≥f（x）；
（3）若关于x的不等式x2+1≥ax+b≥
| 3 |
| 2 |
| 2 |
| 3 |
函数y=f（x）在区间（0，+∞）内可导．导函数f′（x）是减函数，且f′（x）＞0，x0∈（0，+∞）．g（x）=kx+m是y=f（x）在点（x0，f（x0））处的切线方程．
（1）用x0，f（x0），f′（x0）表示m；
（2）证明：当x∈（0，+∞）时，g（x）≥f（x）；
（3）若关于x的不等式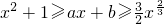
在（0，+∞）上恒成立，其中a，b为实数，求b的取值范围及a，b所满足的关系．
查看习题详情和答案>>
函数y=f（x）在区间（0，+∞）内可导，导函数f'（x）是减函数，且f′（x）＞0。设x0∈（0，+∞），y=kx+m是曲线y=f（x）在点（x0，f（x0））的切线方程，并设函数g（x）=kx+m。
（1）用x0、f（x0）、f′（x0）表示m；
（2）证明：当x0∈（0，+∞）时，g（x）≥f（x）；
（3）若关于x的不等式x2+1≥ax+b≥
在
上恒成立，其中a、b为实数，求b的取值范围及a与b所满足的关系。
查看习题详情和答案>>
（1）用x0、f（x0）、f′（x0）表示m；
（2）证明：当x0∈（0，+∞）时，g（x）≥f（x）；
（3）若关于x的不等式x2+1≥ax+b≥
在上恒成立，其中a、b为实数，求b的取值范围及a与b所满足的关系。
在区间（0，+∞）内可导，导函数
是减函数，且
设
是曲线
在点（
）处的切线方程，并设函数
、
、
表示m；
的不等式
上恒成立，其中a、b为实数，求b的取值范围及a与b所满足的关系.