网址:http://m.1010jiajiao.com/timu_id_81224[举报]
1. C. 由
2. A. 根据汽车加速行驶,匀速行驶,减速行驶结合函数图像可知;
3. A. 由,,;
4. D. ;
5. C. 由;
6. B. 由;
7.D. 由;
8.A. 只需将函数的图像向左平移个单位得到函数的图像.
9.D.由奇函数可知,而,则,当时,;当时,,又在上为增函数,则奇函数在上为增函数,.
10.D.由题意知直线与圆有交点,则.
另解:设向量,由题意知
由可得
11.C.由题意知三棱锥为正四面体,设棱长为,则,棱柱的高(即点到底面的距离),故与底面所成角的正弦值为.
另解:设为空间向量的一组基底,的两两间的夹角为
长度均为,平面的法向量为,
则与底面所成角的正弦值为.
12.B.分三类:种两种花有种种法;种三种花有种种法;种四种花有种种法.共有.
13.答案:9.如图,作出可行域,
作出直线,将平移至过点处
时,函数有最大值9.
14. 答案:2.由抛物线的焦点坐标为
为坐标原点得,,则
与坐标轴的交点为,则以这三点围成的三角形的面积为
15.答案:.设,则
16.答案:.设,作
,则,为二面角的平面角
,结合等边三角形
与正方形可知此四棱锥为正四棱锥,则
,
故所成角的余弦值
则点,
,
则,
故所成角的余弦值.
17.解析:(Ⅰ)在中,由正弦定理及
可得
即,则;
(Ⅱ)由得
当且仅当时,等号成立,
18.解:(1)取中点,连接交于点,
,,
.
,
,,即,
面,.
(2)在面内过点作的垂线,垂足为.
,,面,,
则即为所求二面角的平面角.
,,,
,则,
,即二面角的大小.
19. 解:(1)求导:
当时,,,在上递增
当,求得两根为
即在递增,递减,
递增
(2),且解得:
20.解:(Ⅰ)解:设、分别表示依方案甲需化验1次、2次。
、表示依方案乙需化验2次、3次;
表示依方案甲所需化验次数不少于依方案乙所需化验次数。
依题意知与独立,且
∴
(Ⅱ)的可能取值为2,3。
;
∴
∴(次)
21. 解:(Ⅰ)设,,
由勾股定理可得:
得:,,
由倍角公式,解得,则离心率.
(Ⅱ)过直线方程为,与双曲线方程联立
将,代入,化简有
将数值代入,有,解得
故所求的双曲线方程为。
22. 解析:
(Ⅰ)证明:,
故函数在区间(0,1)上是增函数;
(Ⅱ)证明:(用数学归纳法)(i)当n=1时,,,
由函数在区间是增函数,且函数在处连续,则在区间是增函数,,即成立;
(?)假设当时,成立,即
那么当时,由在区间是增函数,得
.而,则,
,也就是说当时,也成立;
根据(?)、(?)可得对任意的正整数,恒成立.
(Ⅲ)证明:由.可得
1, 若存在某满足,则由⑵知:
2, 若对任意都有,则
,即成立.
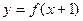 的图像与函数
的图像与函数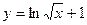 的图像关于直线
的图像关于直线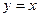 对称,则
对称,则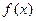 =( )
=( )


