摘要：2．重视通性通法.加强解题指导.提高解题能力 在二轮复习中.不能仅仅复习概念和性质.还应该以典型的例题和习题(可以选用04年的各地高考试题和近两年的各地高考模拟试题)为载体.在二轮复习中强化各类问题的常规解法.使学生形成解决各种类型问题的操作范式．数学学习是学生自主学习的过程.解题能力只有通过学生的自主探究才能掌握．所以.在二轮复习中.教师的作用是对学生的解题方法进行引导.点拨和点评.只有这样.才能够实施有效复习．
网址：http://m.1010jiajiao.com/timu_id_78030[举报]
已知正项数列
的前n项和
满足：
，
（1）求数列的通项
和前n项和；
（2）求数列
的前n项和
；
（3）证明：不等式 
对任意的
，
都成立．
【解析】第一问中，由于所以
两式作差
，然后得到
从而
得到结论
第二问中，
利用裂项求和的思想得到结论。
第三问中，
又
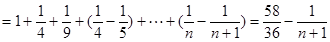
结合放缩法得到。
解：（1）∵ ∴
∴
∴
∴ ………2分
又∵正项数列，∴
∴
又n=1时，
∴
∴数列是以1为首项，2为公差的等差数列……………3分
∴
…………………4分
∴
…………………5分
（2）
…………………6分
∴
…………………9分
（3）
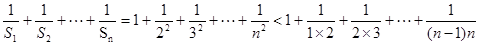
…………………12分
又
，
∴不等式 对任意的，都成立．
查看习题详情和答案>>
我们已学过的算法有求解一元二次方程的求根公式，加减消元法求二元一次方程组解，二分法求函数零点等．对算法的描述有
①对一类问题都有效；
②对个别问题有效；
③计算可以一步步地进行，每一步都有惟一的结果；
④是一种通法，只要按部就班地做，总能得到结果．
以上正确描述算法的有
- A.1个
- B.2个
- C.3个
- D.4个
阅读下面所给材料：已知数列{an}，a1=2，an=3an-1+2，求数列的通项an．
解：令an=an-1=x，则有x=3x+2，所以x=-1，故原递推式an=3an-1+2可转化为：
an+1=3（an-1+1），因此数列{an+1}是首项为a1+1，公比为3的等比数列．
根据上述材料所给出提示，解答下列问题：
已知数列{an}，a1=1，an=3an-1+4，
（1）求数列的通项an；并用解析几何中的有关思想方法来解释其原理；
（2）若记Sn=
，求
Sn；
（3）若数列{bn}满足：b1=10，bn+1=100bn3，利用所学过的知识，把问题转化为可以用阅读材料的提示，求出解数列{bn}的通项公式bn． 查看习题详情和答案>>
解：令an=an-1=x，则有x=3x+2，所以x=-1，故原递推式an=3an-1+2可转化为：
an+1=3（an-1+1），因此数列{an+1}是首项为a1+1，公比为3的等比数列．
根据上述材料所给出提示，解答下列问题：
已知数列{an}，a1=1，an=3an-1+4，
（1）求数列的通项an；并用解析几何中的有关思想方法来解释其原理；
（2）若记Sn=
| n |
 |
| k=1 |
| 1 |
| lg(ak+2)lg(ak+1+2) |
| lim |
| n→∞ |
（3）若数列{bn}满足：b1=10，bn+1=100bn3，利用所学过的知识，把问题转化为可以用阅读材料的提示，求出解数列{bn}的通项公式bn． 查看习题详情和答案>>