网址:http://m.1010jiajiao.com/timu_id_78023[举报]
某市投资甲、乙两个工厂,2011年两工厂的产量均为100万吨,在今后的若干年内,甲工厂的年产量每年比上一年增加10万吨,乙工厂第 年比上一年增加
年比上一年增加 万吨,记2011年为第一年,甲、乙两工厂第
万吨,记2011年为第一年,甲、乙两工厂第 年的年产量分别为
年的年产量分别为 万吨和
万吨和 万吨.
万吨.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)若某工厂年产量超过另一工厂年产量的2倍,则将另一工厂兼并,问到哪一年底,其中哪一个工厂被另一个工厂兼并.
【解析】本试题主要考查数列的通项公式的运用。
第一问由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98
第二问,考查等差数列与等比数列的综合,考查用数列解决实际问题,其步骤是建立数列模型,进行计算得出结果,再反馈到实际中去解决问题.由于比较两个工厂的产量时两个函数的形式较特殊,不易求解,故采取了列举法,数据列举时作表格比较简捷.
解:(Ⅰ)由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98……6分
(Ⅱ)由于n,各年的产量如下表
n 1 2 3 4 5 6 7 8
an 100 110 120 130 140 150 160 170
bn 100 102 106 114 130 162 226 354
2015年底甲工厂将被乙工厂兼并
查看习题详情和答案>>
已知数列{ }中,
}中,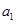 =1,前n项和
=1,前n项和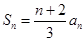 。
。
(Ⅰ)求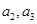
(Ⅱ)求{ }的通项公式。
}的通项公式。
【解析】本试题主要考查了数列的通项公式与数列求和的相结合的综合运用。

【点评】试题出题比较直接,没有什么隐含的条件,只要充分利用通项公式和前n项和的关系式变形就可以得到结论。
查看习题详情和答案>>
(1)求数列{an}与数列{bn}的通项公式;
(2)在数列{an}的任意相邻两项ak与ak+1之间插入k个(-1)kbk(k∈N*)后,得到一个新的数列{cn}.求数列{cn}的前2012项之和.
| 3 |
(1)若N(x0,y0)在椭圆C上,判断椭圆C与它的“伴随直线”的位置关系(当直线与椭圆的交点个数为0个、1个、2个时,分别称直线与椭圆相离、相切、相交),并说明理由;
(2)命题:“若点N(x0,y0)在椭圆C的外部,则直线l与椭圆C必相交.”写出这个命题的逆命题,判断此逆命题的真假,说明理由;
(3)若N(x0,y0)在椭圆C的内部,过N点任意作一条直线,交椭圆C于A、B,交l于M点(异于A、B),设
| MA |
| AN |
| MB |
| BN |