摘要:⑵平行六面体是棱柱中的一类重要的几何体.要理解并掌握“平行六面体 直平行六面体 长方体 正四棱柱 正方体 这一系列中各类几何体的内在联系和区别.⑶须从棱柱的定义出发.根据第一章的相关定理对棱柱的基本性质进行分析推导.以求更好地理解.掌握并能正确地运用这些性质.⑷关于平行六面体.在掌握其所具有的棱柱的一般性质外.还须掌握由其定义导出的一些其特有的性质.如长方体的对角线长定理是一个重要定理并能很好地掌握和应用.还须注意.平行六面体具有一些与平面几何中的平行四边形相对应的性质.恰当地运用平行四边形的性质及解题思路去解平行六面体的问题是一常用的解题方法.⑸多面体与旋转体的问题离不开构成几何体的基本要素点.线.面及其相互关系.因此.很多问题实质上就是在研究点.线.面的位置关系.与第一部分的问题相比.唯一的差别就是多了一些概念.比如面积与体积的度量等.从这个角度来看.点.线.面及其位置关系仍是我们研究的重点. 7.经纬度及球面距离⑴根据经线和纬线的意义可知.某地的经度是一个二面角的度数.某地的纬度是一个线面角的度数.设球O的地轴为NS.圆O是0°纬线.半圆NAS是0°经线.若某地P是在东经120°.北纬40°.我们可以作出过P的经线NPS交赤道于B.过P的纬线圈圆O1交NAS于A.那么则应有:∠AO1P=120° .∠POB=40°.⑵两点间的球面距离就是连结球面上两点的大圆的劣弧的长.因此.求两点间的球面距离的关键就在于求出过这两点的球半径的夹角.例如.可以循着如下的程序求A.P两点的球面距离.
网址:http://m.1010jiajiao.com/timu_id_77999[举报]
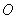 是平行四边形
是平行四边形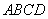 对角线的交点,若
对角线的交点,若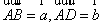 ,则
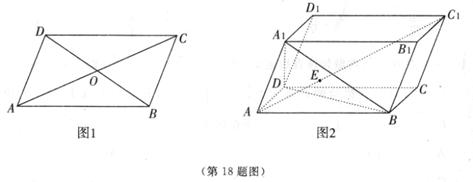
,则 ,(2)在图2所示的平行六面体(底面是平行四边形的棱柱)
,(2)在图2所示的平行六面体(底面是平行四边形的棱柱)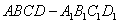 中,
中,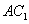 与截面
与截面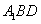 的交点为
的交点为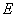 ,设
,设 。类比(1)写出用
。类比(1)写出用 表示
表示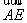 的关系式是 。
的关系式是 。