摘要:26.在学习勾股定理时.我们学会运用图(1)验证它的正确性,图中大正方形的面积可表示为.也可表示为.即.由此推出勾股定理.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法.简称“无字证明 .
网址:http://m.1010jiajiao.com/timu_id_762762[举报]
在学习勾股定理时,我们学会运用图(I)验证它的正确性;图中大正方形的面积可表示为:
(a+b)2,也可表示为:c2+4•(
ab),
即(a+b)2=c2+4•(
ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
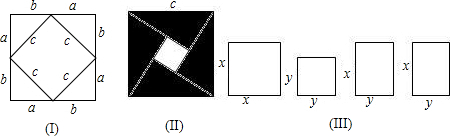
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等);
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证(x+y)2=x2+2xy+y2;
(3)请你自己设计图形的组合,用其面积表达式验证:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq. 查看习题详情和答案>>
(a+b)2,也可表示为:c2+4•(
| 1 |
| 2 |
即(a+b)2=c2+4•(
| 1 |
| 2 |

(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等);
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证(x+y)2=x2+2xy+y2;
(3)请你自己设计图形的组合,用其面积表达式验证:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq. 查看习题详情和答案>>
在学习勾股定理时,我们学会运用图(I)验证它的正确性;图中大正方形的面积可表示为:
(a+b)2,也可表示为:c2+4•( ab),
ab),
即(a+b)2=c2+4•( ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.

(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等);
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证(x+y)2=x2+2xy+y2;
(3)请你自己设计图形的组合,用其面积表达式验证:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq.
查看习题详情和答案>>
在学习勾股定理时,我们学会运用图(I)验证它的正确性;图中大正方形的面积可表示为:(a+b)2,也可表示为:c2+4·( ab),即(a+b)2=c2+4·(
ab),即(a+b)2=c2+4·(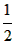 ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”。
ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”。
 ab),即(a+b)2=c2+4·(
ab),即(a+b)2=c2+4·(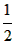 ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”。
ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”。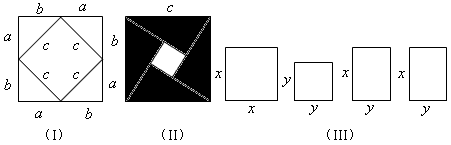
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等);
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证(x+y)2=x2+2xy+y2;
(3)请你自己设计图形的组合,用其面积表达式验证:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq。
查看习题详情和答案>>
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证(x+y)2=x2+2xy+y2;
(3)请你自己设计图形的组合,用其面积表达式验证:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq。
在学习勾股定理时,我们学会运用图(I)验证它的正确性;图中大正方形的面积可表示为![]() ,也可表示为
,也可表示为![]() ,即
,即![]() 由此推出勾股定理
由此推出勾股定理![]() ,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称撐拮种っ鲾.
,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称撐拮种っ鲾.
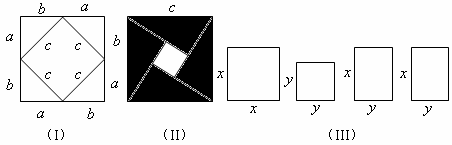
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等).(3分)
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证![]() (3分)
(3分)
(3)请你自己设计图形的组合,用其面积表达式验证:
![]() (4分).
(4分).
(2007•巴中)在学习勾股定理时,我们学会运用图(I)验证它的正确性;图中大正方形的面积可表示为:
(a+b)2,也可表示为:c2+4•( ab),
ab),
即(a+b)2=c2+4•( ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
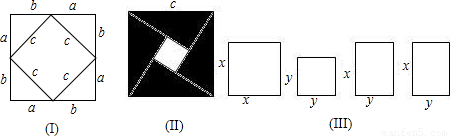
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等);
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证(x+y)2=x2+2xy+y2;
(3)请你自己设计图形的组合,用其面积表达式验证:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq.
查看习题详情和答案>>
(a+b)2,也可表示为:c2+4•(
 ab),
ab),即(a+b)2=c2+4•(
 ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推出勾股定理a2+b2=c2,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等);
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证(x+y)2=x2+2xy+y2;
(3)请你自己设计图形的组合,用其面积表达式验证:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq.
查看习题详情和答案>>