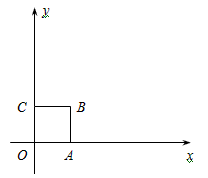
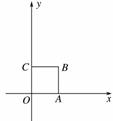
摘要:25.我们知道.当一条直线与一个圆有两个公共点时.称这条直线与这个圆相交.类似地.我们定义:当一条直线与一个正方形有两个公共点时.称这条直线与这个正方形相交.如图.在平面直角坐标系中.正方形OABC的顶点为O.B.(1)判断直线y=x+与正方形OABC是否相交.并说明理由,(2)设d是点O到直线y=-x+b的距离.若直线y=-x+b与正方形OABC相交.求d的取值范围.
网址:http://m.1010jiajiao.com/timu_id_761522[举报]
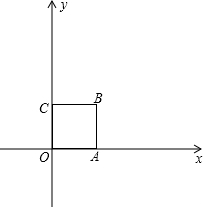 我们知道,当一条直线与一个圆有两个公共点时,称这条直线与这个圆相交.类似地,我们定义:当一条直线与一个正方形有两个公共点时,称这条直线与这个正方形相交.
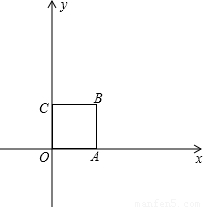
我们知道,当一条直线与一个圆有两个公共点时,称这条直线与这个圆相交.类似地,我们定义:当一条直线与一个正方形有两个公共点时,称这条直线与这个正方形相交.如图,在平面直角坐标系中,正方形OABC的顶点为O(0,0)、A(1,0)、B(1,1)、C(0,1).
(1)判断直线y=
| 1 |
| 3 |
| 5 |
| 6 |
(2)设d是点O到直线y=-
| 3 |
| 3 |
我们知道,当一条直线与一个圆有两个公共点时,称这条直线与这个圆相交.类似地,我们定义:当一条直线与一个正方形有两个公共点时,称这条直线与这个正方形相交.
如图,在平面直角坐标系中,正方形OABC的顶点为O(0,0)、A(1,0)、B(1,1)、C(0,1).
(1)判断直线y= x+
x+ 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;
(2)设d是点O到直线y=-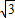 x+b的距离,若直线y=-
x+b的距离,若直线y=-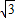 x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
如图,在平面直角坐标系中,正方形OABC的顶点为O(0,0)、A(1,0)、B(1,1)、C(0,1).
(1)判断直线y=
 x+
x+ 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;(2)设d是点O到直线y=-
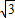 x+b的距离,若直线y=-
x+b的距离,若直线y=-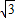 x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围. 查看习题详情和答案>>
查看习题详情和答案>>
我们知道,当一条直线与一个圆有两个公共点时,称这条直线与这个圆相交.类似地,我们定义:当一条直线与一个正方形有两个公共点时,称这条直线与这个正方形相交.
如图,在平面直角坐标系中,正方形OABC的顶点为O(0,0)、A(1,0)、B(1,1)、C(0,1).
(1)判断直线y=![]() x+
x+![]() 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;
(2)设d是点O到直线y=-![]() x+b的距离,若直线y=-
x+b的距离,若直线y=-![]() x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.
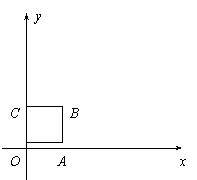
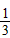 x+
x+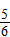 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;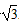 x+b的距离,若直线y=-
x+b的距离,若直线y=-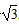 x+b与正方形OABC相交,求d的取值范围。
x+b与正方形OABC相交,求d的取值范围。