摘要:(2)求出?≤时y与x的函数关系式,
网址:http://m.1010jiajiao.com/timu_id_760334[举报]
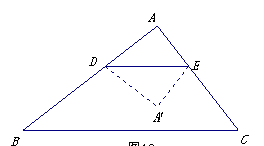
如图,在![]() 中,∠
中,∠![]()
![]() °,
°,![]() ,
, ![]() 的面积为
的面积为![]() ,点
,点![]() 为
为![]() 边上的任意一点(
边上的任意一点(![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() .设
.设![]() 以
以![]() 为折线将△
为折线将△![]() 翻折,所得的
翻折,所得的![]() 与梯形
与梯形![]() 重叠部分的面积记为y.
重叠部分的面积记为y.
(1).用x表示∆ADE的面积;
(2).求出![]()
![]() ≤
≤![]() 时y与x的函数关系式;
时y与x的函数关系式;
(3).求出![]()
![]()
![]() 时y与x的函数关系式;
时y与x的函数关系式;
(4).当![]() 取何值时,
取何值时,![]() 的值最大?最大值是多少?
的值最大?最大值是多少?
 |
查看习题详情和答案>>
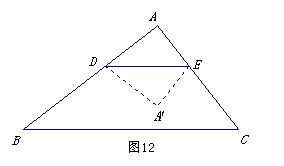
如图,在![]() 中,∠
中,∠![]()
![]() °,
°,![]() ,
, ![]() 的面积为
的面积为![]() ,点
,点![]() 为
为![]() 边上的任意一点(
边上的任意一点(![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() .设
.设![]() 以
以![]() 为折线将△
为折线将△![]() 翻折,所得的
翻折,所得的![]() 与梯形
与梯形![]() 重叠部分的面积记为y.
重叠部分的面积记为y.
(1)用x表示∆ADE的面积;
(2)求出![]() ﹤
﹤![]() ≤
≤![]() 时y与x的函数关系式;
时y与x的函数关系式;
(3)求出![]() ﹤
﹤![]() ﹤
﹤![]() 时y与x的函数关系式;
时y与x的函数关系式;
(4)当![]() 取何值时,
取何值时,![]() 的值最大?最大值是多少?
的值最大?最大值是多少?
 |
 |
查看习题详情和答案>>
如图,在![]() 中,∠
中,∠![]()
![]() °,
°,![]() ,
, ![]() 的面积为
的面积为![]() ,点
,点![]() 为
为![]() 边上的任意一点(
边上的任意一点(![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() .设
.设![]() 以
以![]() 为折线将△
为折线将△![]() 翻折,所得的
翻折,所得的![]() 与梯形
与梯形![]() 重叠部分的面积记为y.
重叠部分的面积记为y.
(1).用x表示∆ADE的面积;
(2).求出![]()
![]() ≤
≤![]() 时y与x的函数关系式;
时y与x的函数关系式;
(3).求出![]()
![]()
![]() 时y与x的函数关系式;
时y与x的函数关系式;
(4).当![]() 取何值时,
取何值时,![]() 的值最大?最大值是多少?
的值最大?最大值是多少?
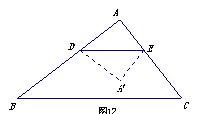
有一项工作,由甲、乙合作完成,工作一段时间后,甲改进了技术,提高了工作效率.设甲的工作量为y甲(件),乙的工作量为y乙(件),甲、乙合作完成的工作量为y(件),工作时间为x(时).y与x之间的部分函数图象如图①所示,y乙与x之间的部分函数图象如图②所示.
(1)分别求出甲2小时、6小时的工作量.
(2)当0≤x≤6时,在图②中画出y甲与x的函数图象,并求出y甲与x之间的函数关系式.
(3)求工作几小时,甲、乙完成的工作量相等.
(4)若6小时后,甲保持第6小时的工作效率,乙改进了技术,提高了工作效率.当x=8时,甲、乙之间的工作量相差30件,求乙提高工作效率后平均每小时做多少件.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)分别求出甲2小时、6小时的工作量.
(2)当0≤x≤6时,在图②中画出y甲与x的函数图象,并求出y甲与x之间的函数关系式.
(3)求工作几小时,甲、乙完成的工作量相等.
(4)若6小时后,甲保持第6小时的工作效率,乙改进了技术,提高了工作效率.当x=8时,甲、乙之间的工作量相差30件,求乙提高工作效率后平均每小时做多少件.
 查看习题详情和答案>>
查看习题详情和答案>>
 甲、乙两个工程队同时挖掘两段长度相等的隧道,如图是甲、乙两队挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:
甲、乙两个工程队同时挖掘两段长度相等的隧道,如图是甲、乙两队挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题: