摘要:20.如下图.已知∠1=∠2.∠C=∠D.求证:AC=BD.
网址:http://m.1010jiajiao.com/timu_id_759794[举报]
(本题8分)如图,已知点P是反比例函数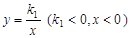 图像上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数
图像上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数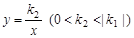 图像于E、F两点.
图像于E、F两点.
(1) 用含k1、k2的式子表示以下图形面积:
① 四边形PAOB;② 三角形OFB;③ 四边形PEOF;
(2) 若P点坐标为(-4,3),且PB︰BF=2︰1,分别求出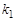 、
、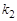 的值.
的值.

查看习题详情和答案>>
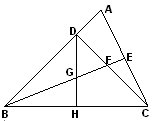
(本题10分)如图,已知在等腰直角三角形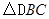 中,
中,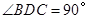 ,
, 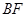 平分
平分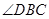 ,与
,与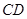 相交于点
相交于点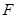 ,延长
,延长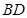 到
到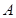 ,使
,使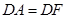 ,
,
【小题1】(1)试说明: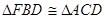 ;
;
【小题2】(2)延长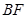 交
交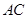 于
于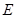 ,且
,且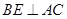 ,)试说明:
,)试说明: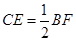 ;
;
【小题3】(3)在⑵的条件下,若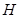 是
是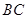 边的中点,连结
边的中点,连结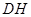 与
与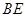 相交于点
相交于点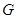 .
.
试探索 ,
,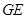 ,
,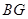 之间的数量关系,并说明理由
查看习题详情和答案>>
之间的数量关系,并说明理由
查看习题详情和答案>>
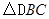 中,
中,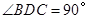 ,
, 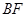 平分
平分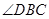 ,与
,与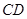 相交于点
相交于点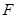 ,延长
,延长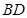 到
到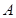 ,使
,使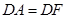 ,
,
【小题1】(1)试说明:
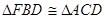 ;
;【小题2】(2)延长
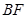 交
交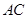 于
于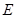 ,且
,且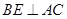 ,)试说明:
,)试说明: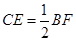 ;
;【小题3】(3)在⑵的条件下,若
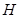 是
是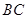 边的中点,连结
边的中点,连结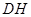 与
与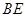 相交于点
相交于点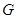 .
.试探索
 ,
,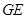 ,
,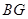 之间的数量关系,并说明理由
查看习题详情和答案>>
之间的数量关系,并说明理由
查看习题详情和答案>>
 27、尺规作图题(保留作图痕迹,不写作法,共5分)
27、尺规作图题(保留作图痕迹,不写作法,共5分) ∴CE∥BF(_______________________________)
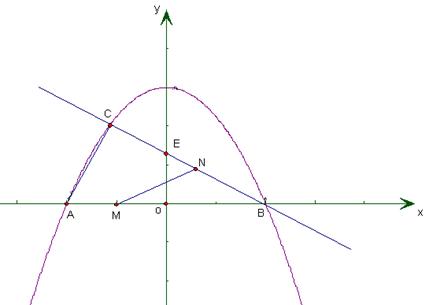
∴CE∥BF(_______________________________)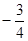 x2+3与x轴交于点A、B,与直线y=
x2+3与x轴交于点A、B,与直线y=