摘要:23.
网址:http://m.1010jiajiao.com/timu_id_758428[举报]
(本题满分11分)
如图所示,⊙![]() 的直径
的直径![]() ,
,![]() 和
和![]() 是它的两条切线,
是它的两条切线,![]() 为射线
为射线![]() 上的动点(不与
上的动点(不与![]() 重合),
重合),![]() 切⊙
切⊙![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() .
.

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若⊙![]() 与⊙
与⊙![]() 外切,且⊙
外切,且⊙![]() 分别与
分别与![]()
相切于点![]() ,求
,求![]() 为何值时⊙
为何值时⊙![]() 半径为1.
半径为1.
查看习题详情和答案>>
(本题满分11分)
如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
【小题1】(1)连接GD,求证:△ADG≌△ABE;(2分)
【小题2】(2)连接FC,观察并猜测∠FCN的度数,并说明理由;(3分)
【小题3】(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.(4分)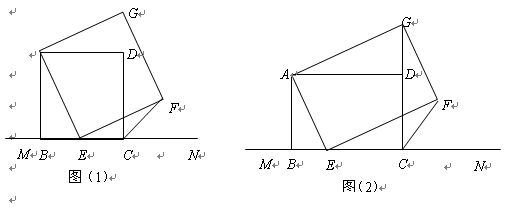
(本题满分11分)
如图所示,⊙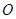 的直径
的直径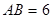 ,
, 和
和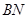 是它的两条切线,
是它的两条切线,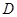 为射线
为射线 上的动点(不与
上的动点(不与 重合),
重合), 切⊙
切⊙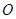 于
于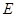 ,交
,交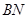 于
于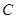 ,设
,设 .
.
(1)求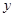 与
与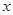 的函数关系式;
的函数关系式;
(2)若⊙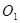 与⊙
与⊙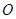 外切,且⊙
外切,且⊙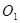 分别与
分别与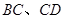
相切于点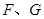 ,求
,求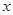 为何值时⊙
为何值时⊙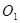 半径为1.
查看习题详情和答案>>
半径为1.
查看习题详情和答案>>
如图所示,⊙
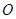 的直径
的直径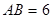 ,
, 和
和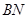 是它的两条切线,
是它的两条切线,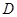 为射线
为射线 上的动点(不与
上的动点(不与 重合),
重合), 切⊙
切⊙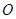 于
于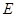 ,交
,交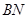 于
于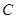 ,设
,设 .
.
(1)求
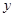 与
与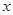 的函数关系式;
的函数关系式;(2)若⊙
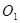 与⊙
与⊙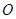 外切,且⊙
外切,且⊙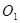 分别与
分别与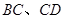
相切于点
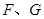 ,求
,求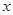 为何值时⊙
为何值时⊙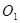 半径为1.
查看习题详情和答案>>
半径为1.
查看习题详情和答案>>
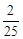 ,得到黄球的概率为
,得到黄球的概率为 ,得到绿球的概率为
,得到绿球的概率为 .已知暗箱中黑球有15个,问袋中原有红球、黄球、绿球各多少个?
.已知暗箱中黑球有15个,问袋中原有红球、黄球、绿球各多少个? 且过顶点C(0,5)(长度单位:m)
且过顶点C(0,5)(长度单位:m)