摘要：9．如图.在平面直角坐标系中.已知OA=OB.B.那么轴上的点A的坐标是
网址：http://m.1010jiajiao.com/timu_id_757529[举报]
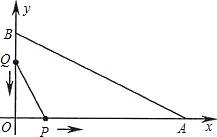如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米．点P从点O开始沿OA边向点A以1厘米/秒的速度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6），那么（1）设△POQ的面积为y，求y关于t的函数解析式；
（2）当△POQ的面积最大时，将△POQ沿直线PQ翻折后得到△PCQ，试判断点C是否落在直线AB上，并说明理由；
（3）当t为何值时，△POQ与△AOB相似． 查看习题详情和答案>>
如图，在平面直角坐标系内，已知OA=OB=2，∠AOB=30°．（1）点A的坐标为（
-1
-1
，| 3 |
| 3 |
（2）将△AOB绕点O顺时针旋转a度（0＜a＜90）．
①当a=30时，点B恰好落在反比例函数y=
| k |
| x |
②在旋转过程中，点A、B能否同时落在上述反比例函数的图象上？若能，求出a的值；若不能，请说明理由．
如图，在平面直角坐标系中，已知OA=| 5 |
（1）点A的坐标是
（-2，-1）
（-2，-1）
；（2）点A关于原点O的对称点A′的坐标是
（2，1）
（2，1）
，并在平面直角坐标系中画出点A′；（3）如果点B在x轴上，且△A′BO是等腰三角形，请写出两个符合条件的点B的坐标：B1
（4，0）
（4，0）
，B2（-
，0）
| 5 |
（-
，0）
，那么S△A′B1O=| 5 |
2
2
，S△A′B2O=
| ||
| 2 |
| ||
| 2 |
如图，在平面直角坐标系中，已知OA=12 cm，OB=6 cm，点P从O点开始沿OA边向点A以1 cm/s的速度移动；点Q从点B开始沿BO边向点O以1 cm/s的速度移动，如果P、Q同时出发，用t(s)表示移动的时间(0≤t≤6)，那么：
(1)设△POQ的面积为y，求y关于t的函数解析式．
(2)当△POQ的面积最大时，△POQ沿直线PQ翻折后得到△POQ，试判断点C是否落在直线AB上，并说明理由．
(3)当t为何值时，△POQ与△AOB相似？
(1)设△POQ的面积为y，求y关于t的函数解析式．
(2)当△POQ的面积最大时，△POQ沿直线PQ翻折后得到△POQ，试判断点C是否落在直线AB上，并说明理由．
(3)当t为何值时，△POQ与△AOB相似？
