摘要：∴S四边形ABCD=SACD+SABC=AC?PD+AC?PB=AC ?=AC?BD 解答问题:(1)上述证明得到的性质可叙述为 ,(2)如下图2.等腰梯形ABCD中.AD∥BC.对角线AC上BD.且交于点P.AD=3cm.BC=7cm.利用上述性质求梯形的面积.
网址：http://m.1010jiajiao.com/timu_id_753151[举报]
31、如图，在矩形ABCD中，对角线AC与BD相交于点O，（1）画出△AOB平移后的三角形，其平移方向为射线AD的方向，平移的距离为线段AD的长．
（2）设（1）中O点平移后的对应点为E，判断四边形CODE的形状．
（3）四边形ABCD是什么四边形时，（2）中的四边形CODE是正方形．
已知M是平行四边形ABCD的边CD的中点，N为AB边上一点，且AN=3NB，连AM、MN分别交BD于E、F（如图①）．
（1）在图②中画出满足上述条件的图形，试用刻度尺在图①、②中量得DE、EF、FB的长度，并填入下表．
由上表可猜想DE、EF、FB间的大小关系是DE=EF=FB．
（2）上述（1）中的猜想DE、EF、FB间的关系成立吗？为什么？
（3）若将平行四边形ABCD改成梯形（其中AB∥CD），且AB=2CD，其它条件不变，此时（1）中猜想DE、EF、FB的关系是否成立？若成立，说明理由；若不成立，求出DE：EF：FB的值．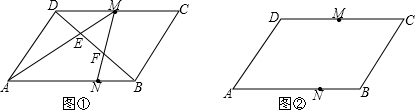
查看习题详情和答案>>
（1）在图②中画出满足上述条件的图形，试用刻度尺在图①、②中量得DE、EF、FB的长度，并填入下表．
| DE的长度 | EF的长度 | FB的长度 | |
| 图①中 | |||
| 图②中 |
（2）上述（1）中的猜想DE、EF、FB间的关系成立吗？为什么？
（3）若将平行四边形ABCD改成梯形（其中AB∥CD），且AB=2CD，其它条件不变，此时（1）中猜想DE、EF、FB的关系是否成立？若成立，说明理由；若不成立，求出DE：EF：FB的值．
查看习题详情和答案>>
6、如图，平行四边形ABCD中，对角线AC，BD相交于点O，将△AOD平移至△BEC的位置，则图中与OA相等的其它线段有（ ）