摘要:解:∴AC⊥BD.∴
网址:http://m.1010jiajiao.com/timu_id_753150[举报]
如图1,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.

(1)在图1中,你发现线段AC,BD的数量关系是
(2)将图1中的△OAB绕点O顺时针旋转90°角,这时(1)中的两个结论是否成立?请做出判断并说明理由.
(3)将图1中的△OAB绕点O顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出判断并说明理由.
解:(2)在图2中,(1)中的两个结论
理由如下:延长CA交BD于点
(2)在图3中,(1)中的两个结论
理由如下:延长CA交BD于点
查看习题详情和答案>>

(1)在图1中,你发现线段AC,BD的数量关系是
相等
相等
,直线AC,BD相交成90
90
度角.(2)将图1中的△OAB绕点O顺时针旋转90°角,这时(1)中的两个结论是否成立?请做出判断并说明理由.
(3)将图1中的△OAB绕点O顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出判断并说明理由.
解:(2)在图2中,(1)中的两个结论
成立
成立
(是否成立);理由如下:延长CA交BD于点
E,∵等腰直角三角形OAB和OCD,
∴OA=OB,OC=OD,
∵AC2=AO2+CO2,BD2=OD2+OB2,
∴AC=BD;
∴△DOB≌△COA(SSS),
∴∠CAO=∠DBO,∠ACO=∠BDO,
∵∠ACO+∠CAO=90°,
∴∠ACO+∠DBO=90°,则∠AEB=90°,即直线AC,BD相交成90°角.
∴OA=OB,OC=OD,
∵AC2=AO2+CO2,BD2=OD2+OB2,
∴AC=BD;
∴△DOB≌△COA(SSS),
∴∠CAO=∠DBO,∠ACO=∠BDO,
∵∠ACO+∠CAO=90°,
∴∠ACO+∠DBO=90°,则∠AEB=90°,即直线AC,BD相交成90°角.
E,∵等腰直角三角形OAB和OCD,
∴OA=OB,OC=OD,
∵AC2=AO2+CO2,BD2=OD2+OB2,
∴AC=BD;
∴△DOB≌△COA(SSS),
∴∠CAO=∠DBO,∠ACO=∠BDO,
∵∠ACO+∠CAO=90°,
∴∠ACO+∠DBO=90°,则∠AEB=90°,即直线AC,BD相交成90°角.
;∴OA=OB,OC=OD,
∵AC2=AO2+CO2,BD2=OD2+OB2,
∴AC=BD;
∴△DOB≌△COA(SSS),
∴∠CAO=∠DBO,∠ACO=∠BDO,
∵∠ACO+∠CAO=90°,
∴∠ACO+∠DBO=90°,则∠AEB=90°,即直线AC,BD相交成90°角.
(2)在图3中,(1)中的两个结论
成立
成立
(是否成立);理由如下:延长CA交BD于点
F
F
,交OD于点E
E
.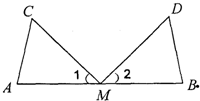 23、如图,M是AB的中点,∠C=∠D,∠1=∠2.说明AC=BD的理由(填空)
23、如图,M是AB的中点,∠C=∠D,∠1=∠2.说明AC=BD的理由(填空)解:∵M是AB的中点,
∴AM=
BM(线段中点的意义)
在△AMC和△BMD中,
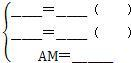
∴△AMC≌△BMD
(AAS
)∴
AC=BD
(全等三角形的对应边相等
) 如图,在△ABC和△DEF中,∠A=∠D,AC=DF,AE=BD,请说明∠C=∠F的理由.
如图,在△ABC和△DEF中,∠A=∠D,AC=DF,AE=BD,请说明∠C=∠F的理由.解:∵AE=BD(已知)
∴AE-BE=
即
在△ABC和△DEF中,
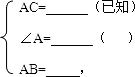
∴△ABC≌
∴∠C=∠F(
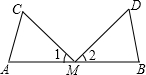 如图,M是AB的中点,∠C=∠D,∠1=∠2,请说明 AC=BD的理由(填空)
如图,M是AB的中点,∠C=∠D,∠1=∠2,请说明 AC=BD的理由(填空)解:∵M是AB的中点,
∴AM=
BM
BM
在△AMC和△BMD中
∠1
∠1
=∠2
∠2
(已知
已知
)∠C
∠C
=∠D
∠D
(已知
已知
)AM=
BM
BM
(已证
已证
)∴△
AMC
AMC
≌△BMD
BMD
∴AC=BD
(全等三角形的对应边相等)
(全等三角形的对应边相等)
.
在学习扇形的面积公式时,同学们推得S扇形=
,并通过比较扇形面积公式与弧长公式l=
,得出扇形面积的另一种计算方法S扇形=
lR.接着老师让同学们解决两个问题:
问题Ⅰ:求弧长为4π,圆心角为120°的扇形面积.
问题Ⅱ:某小区设计的花坛形状如图中的阴影部分,已知AB和CD所在圆心都是点O,弧AB的长为l1,弧CD的长为l2,AC=BD=d,求花坛的面积.
(1)请你解答问题Ⅰ;
(2)在解完问题Ⅱ后的全班交流中,有位同学发现扇形面积公式S扇形=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.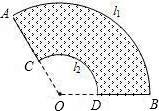 查看习题详情和答案>>
查看习题详情和答案>>
| nπR2 |
| 360 |
| nπR |
| 180 |
| 1 |
| 2 |
问题Ⅰ:求弧长为4π,圆心角为120°的扇形面积.
问题Ⅱ:某小区设计的花坛形状如图中的阴影部分,已知AB和CD所在圆心都是点O,弧AB的长为l1,弧CD的长为l2,AC=BD=d,求花坛的面积.
(1)请你解答问题Ⅰ;
(2)在解完问题Ⅱ后的全班交流中,有位同学发现扇形面积公式S扇形=
| 1 |
| 2 |
| 1 |
| 2 |
 查看习题详情和答案>>
查看习题详情和答案>>