网址:http://m.1010jiajiao.com/timu_id_745345[举报]
 如图,四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形.连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形.
如图,四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形.连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形.(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形;
当四边形ABCD的对角线满足
当四边形ABCD的对角线满足
(2)试证明:S△AEH+S△CFG=
| 1 | 4 |
(3)利用(2)的结论计算:如果四边形ABCD的面积为2012,那么中点四边形EFGH的面积是
如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形。连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形。
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形;
当四边形ABCD的对角线满足_______________时,四边形EFGH为矩形;
当四边形ABCD的对角线满足________________时,四边形EFGH为正方形。
(2)探索△AEH、△CFG与四边形ABCD三者的面积有何等量关系,请写出你发现的结论,并加以证明。
(3)利用(2)的结论计算:如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是 。
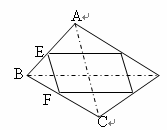
如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形.连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形.
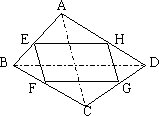
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:
当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形;
当四边形ABCD的对角线满足________时,四边形EFGH为矩形;
当四边形ABCD的对角线满足________时,四边形EFGH为正方形.
(2)探索△AEH、△CFG与四边形ABCD三者的面积有何等量关系,请写出你发现的结论,并加以证明.
(3)利用(2)的结论计算:如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是________.
如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形。连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形。
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形;
当四边形ABCD的对角线满足_______________时,四边形EFGH为矩形;
当四边形ABCD的对角线满足________________时,四边形EFGH为正方形。
(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明。
(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少?
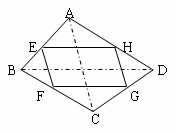
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形.
当四边形ABCD的对角线满足
当四边形ABCD的对角线满足
(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结
 论,并加以证明;
论,并加以证明;(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少? 查看习题详情和答案>>